
South Island, New Zealand

The behavior of water at interfaces is unusual due to its strongly hydrogen-bonded nature and its ability to hold a charge.
![]() Nanobubbles
Nanobubbles
![]() Self-generation of colligative properties in water
Self-generation of colligative properties in water
![]() Silica interfaces
Silica interfaces
![]() The surface of liquid water
The surface of liquid water
![]() The surface of ice (Why is ice slippery?)
The surface of ice (Why is ice slippery?)
![]() Metal interfaces
Metal interfaces
![]() Surface potential
Surface potential
![]() Zeta potential
Zeta potential
![]() Surface charge changes with pH
Surface charge changes with pH
![]() Evaporation and condensation
Evaporation and condensation
![]() Thermodynamics of the liquid-gas surface for water
Thermodynamics of the liquid-gas surface for water
'A surface is a geometrical abstraction and not a physical reality'
W. W. Barkas, 1948
The air-water surface e is a very complex system [2629] and certainly not as simple as often assumed. The surfaces are also extensive with 3.6 ˣ 108 km2 ocean's surface, 1013 km2 cloud and aerosol droplet surface and, ~150 m2 per human lung surface area [3513]. Even as we struggle over the best description for the bulk structuring of water and the water’s interactions with ions and other solutes, the surface of the water is even more challenging [3216]. Nuclear quantum effects of surface water have been reviewed [3138]. Surface water structure varies with temperature, gas molecules binding, ions binding or excluded, electrical gradients forming, and its dielectric and chemistry changes with apparent unpredictability. Further, both sides of the interface have µm thick unstirred layers different from the bulk (gas or liquid) phases. Most surface possesses a two-dimensional hydrogen-bond network [3230], which is clearly different from the bulk-phase three-dimensional network. Further, any surface evaporation causes the formation of helical macrostructures in the surface-water layer (≈ 1 mm) [3194]. It is quite possible that the evaporation processes involve clusters of water molecules (i.e., fog) being removed involving light absorption [4479].
How far do the gas and liquid surfaces extend? Indeed, the volume of liquid water considered ‘surface’ should be electrically neutral, and this is one definition for the surface thickness for water. The interface must include the outer monolayer, the boundary that gives rise to any zeta potential, and any double layer of ions, plus deeper layers where there is surface-influenced anisotropy in either charge or structure. The depth of this surface remains undetermined, but it is likely to be somewhat greater than given by most techniques that look only at a restricted range of selected properties. There is much direct evidence for an effective depth of the liquid surface measured in many nanometers [2751]. Clearly, such a definition of surface depth cannot encompass a charged surface. Therefore, any charge seen on the surface may depend upon the surface layer thickness under consideration. It may well vary between methodologies with different probe depths. Also confusing is that the surface is rough (with ≈ 15% increased surface area [2697] ) rather than planar and is in constant flux rather than thermodynamically static. In a difference to hydrophobic solid/water interfaces, the gas/water surface is not flat, even in the most still conditions. It has nanoscopic surface waves (≈ Å, [2697] ) existing on the water that scatter light with low intensity [2407]. However, energetic considerations indicate that these surface capillary waves are unlikely to be more than about a water diameter high due to water’s high surface tension. In addition to this, several million monolayers exchange with the gas phase every second [2408] and cause evaporation-dependent temperature gradients [2714], so giving rise to long-lasting surface discontinuities and nonequilibrium [2409].
Modeled surface density
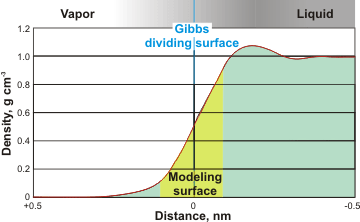
The density, dielectric permittivity [738], and dipole moment of interfacial water change from their bulk water values to those of the gas (five orders of magnitude) over a distance generally regarded as less than about a nanometer. Thus, water’s solvation and ionization properties change at the interface. Most ions and hydrophilic solutes are generally less evident at the interface, but nonpolar gases are more soluble there [1259]. Ions, including hydrogen and hydroxide ions, and other solutes behave differently at the surface to their behavior in the bulk. A critical property of the surface concerns how it affects the local ion distribution. Some ions, such as thiocyanate (SCN− ), azide (N3 −), and iodide (I−) [2778], prefer the surface, whereas others avoid it, as shown by their effects on the surface tension [674] and bubble coalescence [672]. Water at the solid-liquid interface exhibits an anomalously high ionic conductivity up to five orders of magnitude higher than bulk water [4098].
Interfacial water molecules at the gas-liquid surface strongly attract the bulk liquid, causing a high surface tension. Liquid water at liquid-solid and liquid-gas interfaces behaves as a separate thermodynamic system from bulk water [2263]. Liquid water at interfaces can be investigated using x-ray reflectivity [2266], vibrational sum-frequency generation spectroscopy (VSFG) [1468, 3669] and atomic force microscopy [738]. Heterodyne-detected sum-frequency generation spectroscopy of the water surface shows a combination mode (3640 cm−1) of the hydrogen-bonded O-H stretch (~3450 cm−1) and a low-frequency intermolecular vibration (~200 cm−1). This combination band is due to an anharmonic vibrational coupling exclusively at the topmost surface [3647]. Molecular dynamics simulations show, however, that the interface contains a significant amount (>10%) of labile water (with weak O-H hydrogen bonds) that are not easily detectable by the conventional vibrational sum-frequency generation methodology [3668].
Gas at air-water and other gas-water interfaces behaves like a flat hydrophobic surface b. The difference is that the van der Waals interactions between the liquid and gas surfaces are negligible. The surface will be strongly attracted to probes approaching from the gas side at distances of about a micrometer and jumping into contact when still over 100 nm distant [1294], thus showing the long-range nature of the attractive van der Waals forces. Interfacial water absorbs light differently to bulk water, with both absorptions at 270 nm [1328] and 670 nm [2377] being described. The structure of the surface is not entirely understood, but some information has been determined.
The under-coordinated water molecules at the surfaces of both ice and water form similar ice-like, low-density phases that are hydrophobic, stiffer, superfluidic and thermally more stable than the bulk water [2004]. Under pressure at hydrophobic surfaces, liquid water shows increasing ice-like order. However, the pressure response is opposite to that of hexagonal bulk ice, indicating that ice-like order is not to be confused with the presence of natural ice [3399]. Hydrogen-bonding in the surface is stronger than in the bulk [1261] (and this affects the osmotic pressure). However, some hydrogen-bonding is lost, giving a more reactive environment [594] and greater ice nucleation [914]. The increased strength of surface water hydrogen bonds is partially due to the reduced competition from neighboring water molecules [2030] but has little effect on their vibrational lifetime [1262]. This stronger bonding is due to lower anti-cooperativity and compensation for the increased chemical potential on the loss of some bonding. This surface hydrogen bonding gives rise to long-range specific ion effects on the aerial surfaces where tiny amounts of
Sum-frequency vibrational spectroscopy (SFVS) shows that water's libration frequency at the air/water interface is 834 cm−1, compared with the bulk value of ≈ 670 cm−1. In contrast, the OH stretch, time-averaged structure, and ps structural dynamics all show no change [2785]. This indicates that although there is little change in water's hydrogen-bonding length at the interface, these hydrogen bonds are stiffer in their rotation, as happens at other hydrophobic surfaces. SFVS also shows that the doubly donor-acceptor and singly donor-acceptor water molecules are the main hydrogen-bonded species in bulk water, with singly donor-acceptor water molecules the primary species at the air/water interface [2894]. The bending mode signal (~1650 cm−1) is dominated by the surface water molecules at the interface and shows the interfacial organization of water [3789]. It acts as a reporter for the hydrogen-bond strengths of these water molecules. The bending mode frequency at the water/air interface indicates the stronger hydrogen bond of a DD-type (donor-donor) water than that of the D-type water molecule with a free O-H group.
The density, dielectric (permittivity, [738b]), and dipole moment of interfacial water change from their bulk water values to that of the gas over a distance of less than about a nanometer. Thus water’s solvation and dissociation properties also change at the interface, with ions and hydrophilic solutes generally being less soluble but nonpolar gases more soluble [1259]. Ions, including hydrogen and hydroxide ions, and other solutes will behave differently at the surface than in the bulk. Perhaps the most important property of the surface, after the surface tension, concerns how it affects the local ion distribution. Some ions prefer the surface, as shown by their effect on the surface tension (Jones-Ray effect) [674] and bubble coalescence. Both OH− [1025, 1266] and H3O+ [1308] can sit at gas/water interfaces, although clearly not at the same time due to their rapid recombination to form H2O within this lower dielectric interface. As OH− ions are preferred over H3O+ ions (above about pH 3-4), this generally reinforces the interface's negative charge compared with the bulk. Also, any carbon dioxide present forms carbonate and bicarbonate ions with an affinity for aqueous/ hydrophobic surfaces endowing further negative charges [3209, 3304]. It should be noted, however, that no evidence of OH− ions has been found at hydrophobic nanodroplet/water interfaces by sum frequency spectroscopy [2811]. Indeed, the surface pH may be several pH units different from the bulk pH [3405]. Strong acids like HCl and particularly HNO3 re-associate at the interface [2190], allowing their evaporation. However, weak acids, such as formic and acetic acids, have a strong surface preference but dissociate more rapidly when at the surface, reducing evaporation [2787].
Surprisingly, although vibrational sum-frequency generation experiments concluded that both carbonate and bicarbonate anions are largely excluded from the air/water interface, X-ray photoemission spectroscopy suggests a significant accumulation of carbonate below the depletion region outside of the area probed by sum-frequency generation [3304].
An experimental study with foam films of pure water showed stable films with an equilibrium thickness of about 200 nm [3915]. An equation describing the distribution of the electric potential (a modified Poisson-Boltzmann equation) was derived, taking into account of the interaction between ions and the surface. From the concentration dependence of the surface density, it was concluded that OH− ions, and Cl− ions, HCO3−, and CO32− ions adsorb specifically at the water/air interface. Both uncharged ammonia and small carboxylic acids may accumulate at the surface before their evaporation into the gas phase [3615]. Thus the surface is more complex than that suggested by vibrational sum-frequency generation (see elsewhere for a hypothesis).
Interfacial water
As proven by Michael Faraday in 1843 [2471], the ‘natural’ state of such interfaces appears to be negative [1266, 1433, 1477, 1591, 1905, 1951], as at hydrophobic surfaces [1347, 1607]. The interactions of ions [1351], particularly H+ and OH− ions, with the interface have been reviewed [1641]. Chaotropic ions with low surface charge density or high polarizability (such as Cl−, Br−, I−, HO2−, and O2·−, but see ion effects in foams) will favor the gas-liquid interfaces [928a] as they only interact weakly with water (and so can easily lose bound water) but are influenced by the highly polarized surface. Charge transfer causes the surface to reflect the charge on the ions close to the surface [2147], usually anions. Due to charge transfer, the water molecules at the surface may become negatively charged, even when the anion is over 15 Å away from the surface [2147]. An additional effect is charge transfer, where the outside water molecules contain more hydrogen-bond acceptors. In contrast, the water molecules just to the inside of the slip-plane contain an excess of hydrogen-bond donors [2811]. Surface-specific sum-frequency vibrational spectroscopy plus ab initio molecular dynamics simulations on a hexane-water interface show the the OH−'s attraction to this aqueous-hydrophobic interface [4128]. The shimmering buzz of partially charged water molecules at the surface (due to the predominance there of water molecules possessing only three hydrogen bonds) also contribute to the negative surface charge [4456].
Aqueous radicals also prefer to reside at such interfaces [939], as do some molecular species prefer to hydrogen bond on the outside of clathrate-like structures; superoxide c, for example [1260]. The presence of radicals at the surface is further shown by their release when microbubbles collapse [2068]. Excess electrons are stable at the surface of ice for several minutes [1836]. The surface of water possesses redox properties, as shown by the reduction of organic compounds in pure water microdroplets (1 to 50 μm diameter) without using reducing agents, catalysts, or applying external charges [3653].
A combination of kosmotropic/kosmotropic (e.g., LiCl) or chaotropic/ chaotropic (e.g., CsI) ions leads to the formation of ion-pairs at the liquid-air interface. In contrast, there appears to be no, or only small amounts of, such contact ion-pairs in the bulk water [2416]. Li+ behaves differently from other Group I cations (e.g., K+) in that it Li+ adsorbs to the aqueous solution-vapor interface [3081]. This is thought due to the Li+ ion holding onto its entire hydration shell even in the topmost layer of the solution.
Small cations (kosmotropes, but see ion effects in foams) are found away from the interface towards the bulk where their requirement for efficient hydration may be satisfied and as they cannot easily be stripped of the bound water by the interface. Also, a very large electrostatic solvation free energy cost prevents adsorption of low polarizability ions at hydrophobic interfaces such as oils or air [2117]. Such cations only approach the interface in response to the negative surface charge. An exception is the oxonium ion (H3O+), which has a much stronger preference for the surface than other small cations [1500]. In acid solutions, oxonium ions point away from the surface as they only poorly accept hydrogen bonds (but strongly donate three), with their oxygen atom pointing at the surface [1308]. This encourages these ions to sit in the surface layer [1308] in the absence of competing anions such as OH− (see interfacial ions) and can lead to the charging of hydrophobic surfaces in acid solution [1584]. However, at neutral pHs, there is a lower concentration of hydrogen ions than anions at the surface.
Iguazu Falls

The zeta potential of the surface of water is considerable and changes markedly with solute concentration (-65 mV for deionized water [1264], -46 mV for 0.1 mM NaCl, -18.8 mV for 0.1 M NaCl [1265] ). This is due to a surface charge density varying from about an electron per 1000 nm2 for pure water to about an electron per 10 nm2 for 0.1 M NaCl (using the equations from [1267]). The charge at the surface of deionized water with air is similar to that found on small oil droplets in water [711c].j The aerosol mists formed at waterfalls (see left) are negatively charged [2049].
Image charge
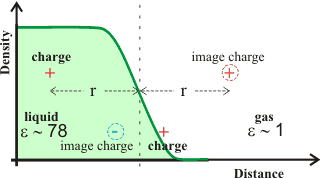
Controlling the approach of ions to the air-water interface is the 'image charge' force, where ions within a dielectric medium are repelled from a dielectric interface towards the bulk liquid by an “image” charge of the same size and polarity (see right). d This repulsion pushes any surface hydroxide ions away from the interface but only by an Ångström or so. If a charge lies on the outside of the interface, its image charge is attractive in the liquid phase, as shown at the bottom of the diagram.
Water in contact with charged interfaces has been reviewed (2021) [4404]. Water coats all hydrophilic surfaces open to ambient atmospheres that are not dried, and the first absorbent layer is generally held firmly. Significantly, this layer will affect the properties of the surface, including their electrical properties, and can cause negative resistance [2223]. The effect of surface binding is sufficient to require an amendment of Archimedes' principle for small bodies, which can then be used to determine the adsorption of water at the surface [3759]. The viscosity of water at hydrophilic surfaces may be orders of magnitude greater than that in the bulk but may be reduced considerably by light (670 nm [2378]). Disrupting the 'unstirred layer' next to a surface has pronounced effects on the surface charge and surface chemistry which can last for several minutes after the stirring has ceased [2138]. Therefore, under flow conditions, all surfaces should be considered dynamic including gas-liquid interfaces with continuous molecular evaporations and condensations.
Putative surface binding of gases
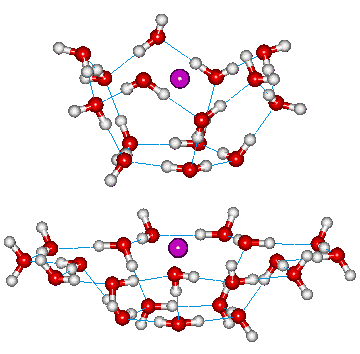
Atomic force microscopy at
air/water interfaces has indicated that the surface
polarization causes the presence of nano-sized clusters of
water a within about 250 nm of the interface [738]. The reduced density and stronger hydrogen bonds within the surface will stabilize water clusters, particularly that of ES over CS full and partial clustering. Small gas molecules bind to these surface clusters due to multiple van der Waals dispersion interactions plus the good fit between the gas molecules and the clusters. In particular, the clusters shown right are particularly stable and may form molecule-holding sites. There is no possibly negative influence caused by the necessary closure of the clusters within the bulk. This explains the greater solubility of the hydrophobic gases at the interface as they can occupy clathrate-type water dodecahedra and pancake-like structures. The water molecule dodecahedra are also thought important in clathrate hydrate formation at liquid-gas interfaces [2563]. This is also supported by the minimal difference in surface density from the bulk density as shown by the abnormally large pressure coefficient of the surface tension (![]() ) [1280] at ambient temperature.
) [1280] at ambient temperature.
The outermost layers of aqueous solutions present a unique material, which shifts most equilibria and where reactions proceed faster than in bulk water [3513]. Interestingly, the air-water interface may give rise to chiral selectivity and recognition [1285]. The surface may, therefore, act as the isotropic bulk cannot. It presents a mechanism for the choice of chirality early in the formation of life's molecules, for example, the D-series of carbohydrates and the L-series of amino acids. Even simple neutral organic pollutants such as phenol have been shown to affect the interfacial water structure significantly [3083]. Molecules that do not bind in bulk water are found to bind at air-water interfaces. Examples of this are the recognition of nucleic acid bases, nucleotides, and amino acids [4158]. In situ optical microscopic observations have revealed that a macroscopic liquid layer denser than bulk water is formed on the surfaces of ice III and ice VI as a water–ice interfacial layer. This high-density liquid layer was separated from bulk water by a clear interface, indicating the presence of two kinds of immiscible structured water [4175].
Very high mobilities of H3O+ and OH− ions have been observed at the water-vapor interface under static electric field orientations of −45° and +45° (relative to the surface plane) and 0.05 V ˣ Å−1. These field orientations are able to pin charges to the vapor interface in addition to dragging them along it [4171].
It has been discovered that the charge on the interface affects the freezing point of supercooled water [1737]. On a surface with no electric field, water droplets were found to freeze at around -12.5 °C. On a positively charged surface, however, the freezing point is raised to -7 °C, while if the surface is negatively charged, the droplet does not freeze until the temperature reaches -18 °C. Whether this strange behavior is due to the reversal of the charge of the natural negatively-charged surface destroying the water clustering has yet to be determined.
The wetting properties of a solid surface depend on the surface topology and are characterized by the length of the surface charge dipoles [3917]. There is a critical length of these charge dipoles, below which they have a negligible effect on wetting. This results from the collective interactions, where the steric exclusion effect between water molecules prevents the water hydrogen atoms from staying close to the negative charges at the same time as the water oxygen atoms stay close to the positive charges. The interface between water and a textured hydrophobic surface can exist in two regimes; either the Wenzel (surface-engulfed) or Cassie-Baxter (water-suspended) state [3548]. At multi-charged surfaces, such as the clay-water interface, the arrangement of the water molecules depends on the density of charges. At low surface charges, the water structuring has low stability and is liquid-like, but the water structuring shows higher stability and is ice-like at high surface charges [3723].
The behavior of water at a graphene electrode surface depends on the applied charge [4455]. There is a sudden rearrangement of the structure of the interfacial aqueous layer (a field-induced phase transition of interfacial water) when the electrode potentials change between negative and neutral or positive. When a negative charge is imposed, the free-hydroxy moiety points towards the graphene. However, if the surface becomes neutral or positive, the free-hydroxy species orient away from graphene and towards bulk water, finding hydrogen bonding partners.
[Back to Top ![]() ]
]
There are reviews concerning the surface of ice [3006] and why it is slippery [1303]. Hexagonal ice is a very soft material (1.5 on the Mohs scale) being scratched by most crystalline solids except soapstone, Mg3Si4O10(OH)2. The surface is liquid below 0 °C (as originally described by Michael Faraday in 1850 [4467]) due to the pressure melting caused by the one-sided attractive interaction with the underlying solid ice [1686]. The solid hexagonal and cubic ice surfaces reorganize to reduce the electrostatic repulsion between non–hydrogen-bonded water molecules and reduce the number and density of the dangling hydrogen atoms [4075]. Using ultrafast surface-specific spectroscopy, the vibrational dynamics of the solidified water molecules at the surface of ice were found to be faster than those of liquid water if hydrogen-bonded but slower and with longer lifetimes if the dangling-OH groups were considered [4077]. There is good evidence that the surface layer is indistinguishable from normal liquid water with a thickness that depends upon the temperature (that is, the further below the freezing point, the thinner the layer; it being many nanometers thick at -1 °C but has almost disappeared by about -38 °C). Other workers report that the surface layer has different flow properties, with much higher viscoelasticity, intermediate between liquid water and ice [3834]. Combined molecular dynamics simulations and sum-frequency generation spectroscopy measurements have shown that hydrogen bonds start to be lost within the topmost ice surface at around -90 °C [3553]. As the temperature rises, this disorder extends to the second layer at around −16 °C, with further bilayer-by-bilayer disorder until the temperature reaches −2 °C. Above this, quasi-liquid droplets and films emerge randomly up to ~100 nm thick on the top of the ice surface dependent on the methodology [3553], with the outer water molecules having less than three hydrogen bonds and acting like 'ball bearings' aiding the slipperiness of the water. There appears to be a weakening of the hydrogen-bonded structure of the outermost water (corrugated) layers on the basal face at 257 K. This has been interpreted as a stepwise change from one to two molten layers [2842]. Indeed, different protocols have given rise to a wide range of apparent thicknesses of this outermost liquid-like layer [3385].
The structure of the surface of ice remains unclear (well-reviewed in [3559]). It has been proposed that the quasi-liquid layer is made up of two-phase types that exhibit different morphologies (droplets and thin layers) [2581]. The surfaces can be examined by laser confocal microscopy combined with differential interference contrast microscopy (LCM-DIM), which can directly visualize the 0.37-nm-thick elementary steps on the ice crystal surface. The nonequilibrium growth of these layers seems to form by the deposition of (critically) supersaturated water vapor onto the ice surface rather than by the surface melting of the ice or the sublimation of ice caused by undersaturated water vapor [2581]. An alternative proposal is that the surface consists of two layers [3221]. In the outer part, both the proton and oxygen sublattices are melted whereas in the inner part only the proton sublattice is melted with the oxygen sublattice stable. Another alternative proposal, using surface-responsive sum-frequency generation spectroscopy, is that the surface layer behaves like supercooled water [3314]. The surface of ice is self-healing, with micrometer deep scratches in the ice surface spontaneously disappearing on a time scale of roughly an hour due to sublimation from and condensation onto the ice surface [4422].
As the surface of ice, near its melting point and exposed to the air, is partially melted, it can take up gases, ions, and organic molecules with ease. Dissolved materials lower the freezing point, and so increase the thickness of the molten layer. Also, reactions take place within this liquid-like phase. However, the pre-melted surface of ice has unique solvation properties, different from those of liquid water, in that ions dissolve but small molecular weight hydrophilic organic molecules, such as glyoxal (O=CH-CH=O), do not [2969]. At low temperatures (≈ 150 K), the melted surface layer has wholly disappeared, and the ice surface is highly ordered. It has two surface-specific vibrational modes at higher frequencies (∼3530 cm−1 and ∼3700 cm−1) [3001]. The vibration at ∼3700 cm−1 corresponds to the free surface hydroxyl group, whereas the ∼3530 cm−1 vibration corresponds to surface water molecules involving the free surface lone pair. Vibrational spectroscopy has found that the basal face of hexagonal ice at 100 K possesses order. One of each surface -O-H groups in its H2O molecules is perpendicular, facing the air (an "H-up" hydrogen ordered surface). At this temperature, there is no quasi-liquid layer on the ice surface. Such ordering is not found in the bulk. However, the hydrogen bond network of water at the surface has more degrees of freedom for molecular translation and rotation, which makes the surface hydrogen ordering possible [3911].
Although ice is often perceived as 'slippery' (for example, ice skating), it is also very 'sticky' (for example, the difficulty in removing ice from car windscreens, the compaction of snow to form 'snowballs' and the ease with which two ice cubes stick together). The underlying slipperiness of ice can be explained by the tetrahedral open structuring [1859] of the liquid water surface that aids the formation of a slipping plane on confinement, whereas its 'stickiness' is due to the refreezing of liquid water confined between ice surfaces, and forming greater than two hydrogen bonds each, so 'fixing' the surfaces disallowing movement. Capillary condensation of liquid water between a tungsten tip and a hydrophobic graphite surface using a friction force microscope has been proposed to form a sticky 'ice' at room temperature [1033]. f These different perceptions depend on the speed of the relative movement between the surfaces and the presence and properties of the ultra-thin layer of quasi-liquid water/amorphous ice on the crystalline surfaces [937] that may be 10 nm thick or greater. This surface layer is easily melted further by frictional heating with the low thermal conductivity of ice, reducing heat loss. Also, there is a deformation of the ice, on skating, due to the pressure and the ease that the ice may deform (plowing). The trails behind the skates are due to both the melting and the plowing. At low skating speeds, the plowing dominates, while at high speeds the friction in the water layer dominates [2944]. Usually, skates are tilted, clearly on curves but also on straights. Such tilted skate edges increase the friction substantially, even for small tilts, and this increase is more pronounced at higher velocities [3797]. Ice-on-ice friction both with and without water on the ice surface has been investigated [3905]. The friction coefficient was little affected at sliding speeds above a cm ˣ s−1, but at lower speeds, the friction coefficient on wet ice was significantly higher than on dry ice.
The stickiness of ice is examined through its adhesion to different surfaces, where low ice adhesion surfaces are included in anti-icing strategies [3791]. The ice adhesion strength decreases from -10°C to -18°C for ice-aluminum surfaces but is almost independent of temperature for a commercial ice-phobic non-stick coating.
The structure and mobility of liquid water at the clay/ice interfaces have been determined. The water molecules within the premelting layer within 4 K below the melting point and less than 2 nm thick form a low-density structure [4331].
[Back to Top ![]() ]
]
The oxygen atoms of water bind to metal atom surfaces whereas the hydrogen atoms hydrogen bond to surface water [2734]. Clean metal surfaces are highly hydrophilic, giving zero contact angles. [3786].
The 100 surface of Pt is four-coordinated,
allowing fully hydrogen-bonding water
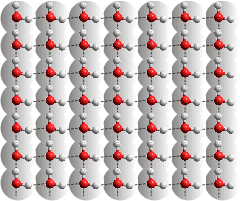
Surface oxide/hydroxide, if present due to the temperature and reactivity of the metal surface, also hydrogen bond to water. The hydrophilic/hydrophobic balance of a metal surface depends on the metal atom packing arrangement and spacing and the interaction time, temperature, and pressure of the water contact. The structures are often uncovered experimentally by the use of scanning tunneling microscopy (STM) [2739].
The binding energy of the water oxygen atoms to the metal atoms Au < Ag < Cu < Pd < Pt < Ru < Rh vary between 12 and 40 kJ ˣ mol−1 [2735], mostly slightly stronger than waters' hydrogen-bonding. The structure of the bound H2O has little change upon adsorption. They preferentially lie flat on the surface due to metal atoms' interactions of their 1b1 p-like lone pair orbitals (perpendicular to the plane of the water molecule) to metal 4d-orbitals [2740].
The 111 surface of Pt is six-coordinated, not
allowing fully hydrogen-bonding water
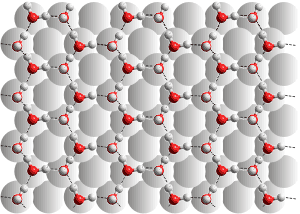
For example, the 100 face of a platinum crystal is four-coordinated, allowing a hydrogen-bonded water sheet to form (see right top [2733]). As this water layer is fully hydrogen-bonded, it creates a surprisingly substantial hydrophobic barrier to further water adhesion.
Any further water added forms spherical droplets on the surface and do not spread. The 111 platinum crystal face (see right) bonds to the most stable flat-on-surface water molecules with about 34 kJ ˣ mol−1. Bonding to the upright water molecules has only 9 kJ ˣ mol−1 stabilization with Pt···O distances of 2.36 Å [2735]). However, the platinum is locally six-coordinated and frustrates water's hydrogen-bonding in the first layer so leaving further bonding sites on the effective hydrophilic surface layer and allowing further water to spread [2733]. The interfacial water molecules can diffuse within layers and exchange with secondary hydrating water through hydrogen bond rearrangements and quantum tunneling. Due to the different binding of the 111 face compared with the 100 face, the relaxation times of water molecules adsorbed on the 111 face are much faster [2736]. The interactions between liquid water with hydroxyl species on Pt(111) surfaces have also been investigated, where the surface is hydrophobic at high hydroxyl coverage [4446].
The hydrophobicity of a naturally hydrophilic Pt-surface depends on its curvature. There is a reversible transition between hydrophobicity and hydrophilicity on going from a flattish surface to a tightly curved surface, with the hydrophobicity caused by the interfacially ordered water [3401]. Water dissociates at the more reactive stepped Pt(221) surface. It has been found that nuclear quantum effects (NQE) are iessential to the partial dissociation of water due to their ability to make many strained conformations thermodynamically competitive [3115].
Low-temperature scanning tunneling microscopy and density functional theory have shown the possibility of many water nano-clusters forming on metallic Cu surfaces. These hydrogen-bonded ring structures resemble the resonance structures of polycyclic aromatic hydrocarbons and allow a refinement of the so-called “2D ice rules”, which have proved helpful in understanding water−ice structures at solid surfaces [2915].
[Back to Top ![]() ]
]
Surface potential convention
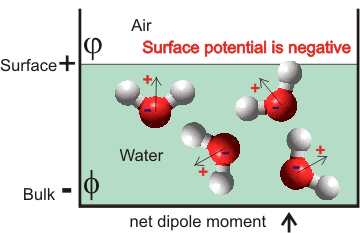
The sign convention for the surface potential is generally taken as measured from the air towards the solution. Therefore, a positive potential (χ, chi) means the bulk is positively charged, and the surface is negatively charged, and a negative potential (see right) means the bulk is negatively charged (Φ, phi. Galvani inner potential) and the surface is positively charged (φ, psi, "Volta" outer potential); Χ = Φ - φ. Most water models give negative surface potentials, but not all workers follow this convention.
Whereas early theoretical works predicted that the surface should be neutral, i experimental data indicates significant surface potential, dependent on the solute salt's concentration. Surface Potential of the Air/Water Interface is subject to a 2020 review [4254].
Static and dynamic aspects of surface potentials are discussed in [3067]. There are several methods available for the determination of surface potentia l[4404]. These methods, such as electrophoretic measurements, atomic force microscopy, and sum- frequency generation (SFG) spectroscopy, depend on the theoretical model chosen.
[Back to Top ![]() ]
]
Nanobubble zeta potential
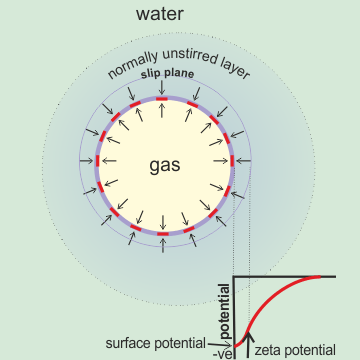
The zeta potential (ζ) is the potential drop in volts across the mobile part of the double layer responsible for movement in an electric field. The zeta potential is positive if the potential increases from the bulk towards the surface. It is due to the apparent effective charge on a moving charged particle and determined from the electrophoretic mobility. Although often proposed to be due to the 'slipping plane' charge, it probably lies well within the unstirred surface layer (except when maximally moved by an electric field) and several water diameters away from the charged surface. It is likely to be close to, if numerically smaller than, the actual surface potential of the nanobubble (particle) as the surface charge is counteracted by a smaller amount of counter-ion held nearby. The key parameter determining the position of the slip plane and the ζ-potential of colloids is the surface hydration. Although the exact physical meaning of the ζ-potential is unclear, it does indicate the electrostatic interaction between particles. The zeta potential keeps similarly charged particles apart, and when it is counteracted, the particles often coalesce (flocculate). The unstirred layer also marks the vicinity of the surface where the concentrations are different from their value in the bulk solution (the diffusioin layer of thickness the Debye length, κ−1 ).
Zeta potential is readily determined from the movement of such particles in an electric field and depends on the relative permittivity (dielectric constant) and viscosity. It is calculated using the Smoluchowski equation.
![]()
where νE is the electrophoretic mobility, ε0 is the relative permittivity, εr is the electrical permittivity of a vacuum, ζ is the zeta potential, μ is the solution viscosity, r is the particle radius, η0 is the bulk ionic concentration, z is the valence of the ion, e is the charge of an electron, kB is the Boltzmann constant and T is the absolute temperature. There is a problem distinguishing the zeta potential of similarly sized sub-micron bubbles and particles in solution; thus, zeta potentials of such solutions would be mixed.
Zeta potential of latex with changes with CsCL and LiCl
from [3564]
![Zeta potential of latex with changes with CsCL and LiCl, from [3564] Zeta potential of latex with changes with CsCL and LiCl, from [3564]](images/zetasalt.gif)
The zeta potential varies with ionic strength and the salt(s) present [3564], varying in line with the Hofmeister series but differing in the direction at high and low concentrations (see right). The weakly hydrated (the most chaotropic, e.g., Cs+) ions adsorb better to hydrophobic surfaces compared to the most strongly hydrated (the most kosmotropic, e.g., Li+) ions. Ions are increasingly accumulated in the innermost layer (the Stern layer), resulting in a substantial decrease in the electrophoretic mobility and consequent increase in the ζ-potential with concentration at low concentrations (see right). The variation of ζ-potentials with salt concentrations gives a maximum as, at higher concentrations, the electrical double layer is compressed at high ionic strength, causing a decrease in the ζ-potential [3564]. Similar effects are found with hydrophilic particles but with the maximum occurring at about ten-fold higher concentrations
The zeta potential changes with pH, and there will be a pH at which it is zero, the isoelectric point. Colloids are least stable at this isoelectric point and, generally, most stable at higher positive or negative zeta potentials found at more extreme pH.
[Back to Top ![]() ]
]
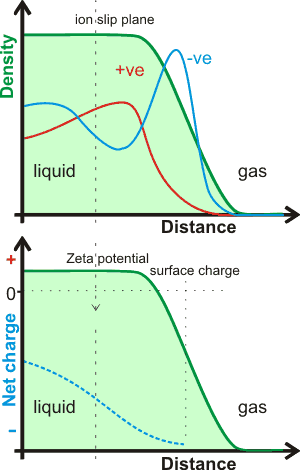
Interfacial water surface density and charge profiles
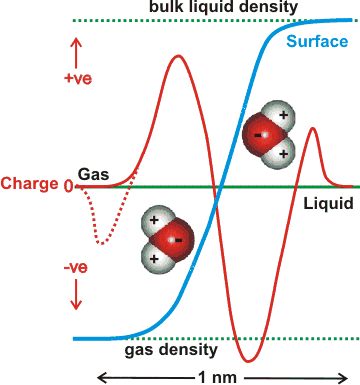
The charge on the surface of theoretically modeled water without dissociation changes the charge across the surface that depends on the depth of the surface examined, as indicated opposite [1348a]. Thus overall, it is negative (relative to a positive bulk) but where the very outer layer of the interface (next to the gas) is more positive [1348c]. The outer (gas-facing) positive contribution is due to the almost-free singly-linked water molecules compensating for the negative quadrupole and dipole contributions in the denser part of the surface layer [1348b]. An explicit ab initio electronic charge density study shows that a negative exterior surface may be present due to electron density 'leaking' into the gas phase (suggested by the dotted line opposite), and not because of any preferential orientation of water molecules [1721]. However, this may have a consequential orientation effect similar to the description above.
There is some dispute over the charge at aqueous surfaces [1205, 2628], with much of the extensive earlier work indicating negative [1517]. It should be noted that the vibrational sum frequency spectroscopy of the broad and nonzero signal intensity between 1700 and 3000 cm−1 showed no evidence for the adsorption of either H+ or OH− in a pH range extending between at least pH 2 and pH 11 [3488]. Molecular modeling is restrictive to the number of molecules used and usually has just a single ion (H3O+ or OH−) with a few (e.g., a thousand or so) water molecules. It should be recognized that such situations are far from realistic as there are no counter-ion effects, the pH's are effectively extreme (pH ≈ 1 for H3O+), and the particles are charged; such models usually give the H3O+ on the surface with the OH− ion buried [2577]. Also, simulations have shown that NaOH solution surfaces are negative [1677]. Stable nanoscopic droplets of water have been formed with 0.005 e− nm−2 negative charge [2298]. The undisputedly negative zeta potential greatly influences the view prominent here [1591]. Also, there are good reasons to suppose that the negative surface region is a different aqueous phase, perhaps similar to a liquid crystal, that extends for up to hundreds of nanometers or even further [1328a]. It is possible that this aqueous phase is created by the higher osmotic pressure created at the surface (e.g., see [1669]) by an excess of longer-lived water clusters created there.
It is challenging to keep the surface of water uncontaminated during experiments. Tiny amounts of contaminants in the solution or gas phase tend to gather here. For example, the dissolution of atmospheric CO2 generates HCO3− and H3O+. These ions result in interfacial charge separation, with negatively charged ions accumulating at the interface and hydrogen cations diffusing to the bulk [3858].
[Back to Top ![]() ]
]
Zeta potential of water over a range of pH, from [1853]
![Zeta potential of water over a range of pH, [1853] Zeta potential of water over a range of pH, [1853]](images/zeta_potential.gif)
There is some dispute over the charge on the surface at pH 7 [1205]. Part of this dispute may be due to the ambiguity in what is meant by 'surface'; is it the very outside, or is it several molecular dimensions deep as found with the 'slipping plane'. Shown opposite is the zeta potential in water with no added ions except the necessary H3O+ and OH− [1853]. The addition of Na+ ions removes the positive peak and reduces the zeta potential at higher pHs.
In dilute HCl, the interfacial hydrated proton experimentally shows substantial interfacial stabilization by -5.44±0.84 kJ ˣ mol−1 [3843]. Oxonium ions (H3O+) may well favor the extreme outside surface layer as they are anisotropic (as also are hydroxide ions). However, this layer has low molecular density, and any net acidity would be diluted by several orders of magnitude if the entire surface layer (that is, the molecules from the surface down to those showing 'bulk' properties) was to be considered. Also, they may attract hydroxide ions and eliminate their charge by forming water. Using acid concentrations (HCl, HBr, HI) in the range 1 - 300 mM (i.e., pH 0 - 3), it has also been found that the surface adsorption of hydronium ions is independent of any specific proton-halide anion interactions and follows a constant adsorption free energy, DG ~ –3.74 (±0.56) kJ ˣ mol−1 corresponding to a reduction of the surface pH with respect to the bulk value by 0.66 (±0.10).
Surface H3O+ ions may (preferably) evaporate from the surface [1883], leaving a negatively charged surface behind. Throughout this relatively large volume, hydroxide ions are preferred over oxonium ions. In small water cluster modeling, H3O+ seems to prefer the outside of clusters [854], whereas OH− prefers a more central position [1828]. However, such a small cluster modeling approach may not apply to extensive surfaces as optimal small clusters of just H2O do not seem to be present in bulk water. Using a continuum model (where the explicit structure of water is not included) also prefers H3O+ towards the outside of the cut-off surface rather than OH− [2360]. Such a model, however, does not work well in the majority of water studies and does not explain the presence of negatively charged interfaces found by electrophoresis. Studies with surface-active pH-sensitive dyes (e.g., [1947] can show the 'apparent' pH at the surface as different from the bulk pH, but care must be taken over the conclusions as differences may be due to artifacts inherent in the determination as the dye completely covers the surface.
[Back to Top ![]() ]
]

Evaporation is a surface phenomenon where bulk bubbles cannot form as the vapor pressure is lower than the atmospheric pressure. Evaporation differs from boiling, which is a bulk liquid phenomenon where the saturated vapor pressure is equal to the surrounding atmospheric pressure, with bubbles of water vapor forming in the bulk. There is a net evaporation (loss) of liquid water from its surface so long as the surrounding gas phase is not saturated with water vapor (see humidity, air-borne water, and humidity maps). There is net condensation (gain) of liquid water when the surrounding gas phase is saturated with water vapor, and the surface is cooler than the dew point. Under all conditions, however, there is both evaporation and condensation at differently controlled rates. Both are nonequilibrium processes. There is a rapid flux at the surface. About a hundred million water molecules per second impinge each square nanometer at 25 °C. At equilibrium, the same number of molecules leave the liquid phase, with the average residence time for a water molecule on the surface about 0.1 μs.
As evaporation is an endothermic process, it cools the liquid and heats the air. As the specific heat of gaseous water (~34 J ˣ mol−1 ˣ K−1) is one-half that of liquid water (~75 J ˣ mol−1 ˣ K−1), the gas temperature rises twice as much as the water is cooled. Clearly, condensation heats the liquid and cools the air. In an enclosed environment, a liquid will evaporate until the surrounding air is saturated. Above an evaporating aqueous surface, the humid air is less dense than dry air and will, therefore, rise to drive convective currents and change the boundary conditions. Air becomes lighter as we add water to it. It is a mistake to conclude that, as the bulk water cools on evaporation, the boundary gas also cools enough to 'fix' the boundary layer of gas in place, as this gas heats up. On the other hand, the drier air when condensing will be denser and cooler and tend not to move. Condensation commonly occurs when a gas containing vapor is cooled to its saturation limit, such as when warm, humid air inside a dwelling hits a cold external wall. The two processes of evaporation and condensation are not, therefore, the reverse as each other.
Evaporation of water from the oceans keeps the oceans cool and the air warmer. Humid air absorbs infrared energy (the most prominent greenhouse effect) and acts as a blanket at night to keep nights from getting too cold. In low-humidity deserts, even in the tropics, nights can be quite cold without this blanket. As the water vapor content in the air may be restricted by temperature and pressure, moist air may deviate significantly from an ideal gas compared to dry air. Increasing the water vapor in the air, at constant temperature and pressure increases its volume. Evaporation of water from our skin, due to perspiration with subsequent evaporation, keeps us cool. If the relative humidity is high, this process cannot function, and we may become uncomfortably hot. More blood may come to our skin to attempt to cool, less blood goes to the active muscles and the brain, physical strength and alertness decline, in extreme resulting in heatstroke. As an example, if the air temperature is 29 °C (85 °F), a person feels it cooler at 26 °C (78 °F) at zero humidity but much hotter as 42 °C (108 °F) at 100% humidity. Similarly, keeping a house more humid when cold makes it feel warmer. Since it costs a lot less to humidify the air than to heat it, a humidifier saves money.
The mechanism and rates of evaporation and condensation have proved very difficult to model, with orders-of-magnitude different results being produced [2759]. One reason for this is that the processes are rare on modeling timescales, and therefore it’s challenging (expensive) to model those phenomena by computer simulations. A significant complexity in this (generally) nonequilibrium phenomenon is a difference in temperature between the liquid surface and the interfacial vapor, g depending on the vapor pressure and the temperatures of bulk liquid and bulk vapor. Even the direction of the discontinuity has proved contentious. The two empirical parameters used are the condensation and evaporation coefficients, originally defined as:
condensation coefficient = number of molecules absorbed by the liquid phase
number of molecules impinging on the liquid phase
evaporation coefficient = number of molecules transferred to the vapor phase
number of molecules emitted from the liquid phase
Both values are proposed to be between 0 and 1 but may not be constant or equal, even at equilibrium. Also, the values depend on their precise definitions in terms of distance and timescale. The experimental values for these coefficients depend on the underlying theory but may lie orders of magnitude below unity and are very different to each other and between different researchers. The primary reason for the condensation coefficient being less than unity is that impinging molecules may knock out an existing molecule from the liquid or they simply bounce off. The primary reasons for the evaporation coefficient being less than unity is that leaving molecules may bounce back from molecules in the vapor or merely be replaced by vapor molecules [2760]. It is difficult to separate the two processes experimentally, but this can be achieved by using liquid microjets in a vacuum system with evaporation without any condensation.
The evaporative flux (Je , molecules ˣ m−2 ˣ t−1) has been proposed by the Hertz−Knudsen equation: h
Je = ![]()
where A, N, t, α, P, NA, M, R, and T are the area (m2), the number of gas molecules, time (s), evaporation coefficient (dimensionless), saturation vapor pressure (Pa), Avogadro constant (mol−1), the molecular mass of the evaporating molecule (kg ˣ mol−1), gas constant (J ˣ mol−1 ˣ K−1) and temperature of the surface (K) respectively. The validity of the equation has been questioned, and other versions of this equation exist that make different assumptions. Water's surface presents a more complex and anomalous environment than other liquids that is best examined by experiment rather than theory. Also, natural open systems will behave very differently from closed systems, even at equilibrium. Unfortunately, experiments are challenging, and the experimental processes may interfere with the evaporation/condensation processes (e.g., temperature determinations across the interfaces).
The Knudsen layer is the nonequilibrium unstirred layer on the gas side of the gas-liquid interface. The thickness of this layer is several times the mean free path of the mixture. The mean free path is proportional to the (gaseous) viscosity and the square root of the temperature and inversely proportional to the pressure and the square root of the molecular mass of the mixture. At 20 °C and atmospheric pressure, the mean-free path of water vapor and dry air are 2.16 µm and 0.07 µm [2714]. In this layer, intermolecular collisions, including the heavier non-condensable gases present (e.g., O2, N2), cause substantial changes to the velocity distributions [3387].
Water evaporation from aqueous solutions may lead to the build-up of structure(s) and composition gradients at their interface with air,with the evaporation rate decreasing with time(t) as t½ and dependent on the rate of diffusion [3345]. The effect of HCl on the evaporative flux is complex, with an increase of 45% (relative to pure water) in 0.1 M HCl and a decrease of 60% in 1 M HCl [3307].
The evaporation rates of both water droplets and ice crystals are limited by the diffusive transport of the vapor away. Therefore, the evaporation from ice and snow (sublimation) is similar to that of water drops [3446]. The rate of ice crystal sublimation is significant as it has a major impact on global climate since surface ice and snow determine Earth’s albedo. The vapor pressure and evaporation rate of an ideal A:B liquid binary mixture varies linearly with the concentration of A and B species when A:A, A:B, and B:B interactions are identical. When the A:B interactions are stronger than the A:A and B interactions, such as in water-formic acid mixtures, the vapor pressure of water-formic acid mixtures is markedly lower than predicted Raoult’s law, and the evaporation rate is also lower [4356]. However, when these interactions are weaker such as in water-methanol mixtures, the vapor pressure and evaporation rate are markedly higher.
An interesting phenomenon of evaporation is the boiling water challenge. Boiling water tossed into an icy atmosphere (<~ -25 °C) immediately turns to snow. This only works if the water is close to boiling (>~ 93°C; i.e., snow is made using boiling water and not cold or warm water). The water passes through three states almost instantaneously, liquid ![]() gas
gas ![]() liquid
liquid ![]() solid. The hot water evaporates quickly (as it is hot) to gaseous steam, which then cannot be held by the cold atmospheric gas and condenses into a cloud of tiny droplets with large relative surface area per mass, that then freeze to form snow. To supplement natural snow at skiing resorts, snow-makers blow dry air and water into a cold, dry atmosphere where clouds of fine cold droplets cool further by evaporation and freeze to form snow. This artificial snow lasts longer than natural snow as it is more compact and melts more slowly.
solid. The hot water evaporates quickly (as it is hot) to gaseous steam, which then cannot be held by the cold atmospheric gas and condenses into a cloud of tiny droplets with large relative surface area per mass, that then freeze to form snow. To supplement natural snow at skiing resorts, snow-makers blow dry air and water into a cold, dry atmosphere where clouds of fine cold droplets cool further by evaporation and freeze to form snow. This artificial snow lasts longer than natural snow as it is more compact and melts more slowly.
[Back to Top ![]() ]
]
At the liquid-gas surface the following thermodynamic relationship holds:
dG = -SdT + VdP + γdA + Σi μdni
where G, U, S, T, V, P, γ, A, μ and ni are the thermodynamic quantities, Gibbs (free) energy, internal energy, entropy, temperature, volume, pressure, surface tension, surface area, chemical potential and number of moles of substance i, respectively.
From the properties of the differential: ![]() and
and ![]() .
.
Also, there is the Maxwell relation ![]() (see. for example [1287]).
(see. for example [1287]).
Although ![]() has units of length, this may be misleading. It is better to consider its reciprocal
has units of length, this may be misleading. It is better to consider its reciprocal ![]() as a measure of a difference in density between surface and bulk density.
as a measure of a difference in density between surface and bulk density.
As H = G + TS, ![]() then
then ![]() (surface enthalpy).
(surface enthalpy).
From inspection of the surface tension changes with temperature, it is clear that this term (the surface enthalpy) is always positive.
As H = U + PV, ![]()
Also, ![]() where
where ![]() .
.
Therefore, ![]()
The internal (cohesive) pressure (Πi) [1279] is the work required to increase the volume at a constant temperature, a constant external pressure, and constant solute concentrations, having the same units as pressure.
As dU = TdS - PdV, therefore ![]() (see above),
(see above),
and as, the internal pressure may be calculated from (Πi + P) = Tα/βT, where α is the coefficient of thermal expansion and βT is the coefficient of isothermal compressibility [1279].
It follows from
![]() and
and ![]()
that
[1519]
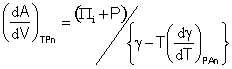 and
and 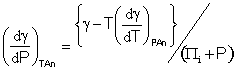
As Tα/βT is zero at 3.984 °C, so is (Πi + P) and both are negative below this temperature, as must be; Πi is zero at 3.99 °C when cohesive and repulsive components of the hydrogen-bonding are equal. It follows that the densities of surface and bulk water are equal at a temperature of 3.984 °C as, below this temperature, the surface density contracts relative to the bulk density (somewhat like what happens at the surface of hexagonal ice [937] ). Thus below a temperature of 3.984 °C, the bulk liquid is less dense than the surface liquid, while above this temperature, the bulk liquid is denser than the surface liquid.
[Back to Top ![]() ]
]
a These clusters are built up from ≈ 100 H2O molecule clusters, the same size that forms the core to the ES clusters in the icosahedral water model [738b] and as found by X-ray analysis in Mo-based nanodrops. [Back]
b A water layer with a thickness of up to 35 nm exists at hydrophobic surfaces. This layer is characterized by a more
ordered network of hydrogen bonds than liquid water [1714]. [Back]
Hydrated superoxide anion, O2·−
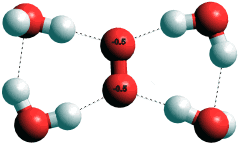
c Superoxide (O2·−) hydrates in a planar manner (see right) to H-O protons on four water molecules [2007]. It decays by reaction with its conjugate acid HO2·,
O2·− + HO2· + H2O → H2O2 + O2 + OH−
in water at a rate constant of about 108 M−1 s−1 which gives a half life-period of about a second, when O2·− and HO2· are at micromolar concentration. [Back]
d The opposite effect occurs at metal or uncharged conductive interfaces, where ions are attracted towards the surface due to oppositely charged 'image' charges. [Back]
e Although sometimes the word surface is limited to its two-dimensional geometrical meaning while the word interface is used to describe the thin three-dimensional layer between the phases in contact, at this site, the two words are used interchangeably to describe the thin three-dimensional layer, including several water layers below the water-air contact line unless further clarified. [Back]
f Such confined meniscus water has been shown to possess 106-107 times greater viscosity than bulk water [1304]. [Back]
g Another study finds that the temperature discontinuity across the evaporating interface is ≤ 0.1 K [3792]. [Back]
h H. Hertz, Ueber die Verdunstung der Flüssigkeiten, insbesondere des Quecksilbers, im luftleeren Raume, 'About the evaporation of liquids, especially mercury, in a vacuum'. Annalen der Physikk und Chemie, 253 (1882) 177-193. [Back]
i L. Onsager and N. N. T. Samaras, The surface tension of Debye-Hückel electrolytes. Journal of Chemical Physics, 2 (1934) 528-536. [Back]
j The source of this negative charge at the oil-water interface has been established (in 2021) as due to the unexpected strong charge-transfer interactions that arise from interfacial C–H∙∙∙O hydrogen bonds [4385]. Water at the oil-water interface had a stronger hydrogen bonding compared with the air-water interface. The negative charge transfer from water to oil explained the negative charge, negative zeta-potential, and stability of the bare oil droplets, with the water's hydrogen atoms buried in the oil at the interface and forming many weak hydrogen bonds between oil and water. [Back]
Home | Site Index | Nanobubbles | Confined water | Solubility of nonpolar gases | Surface tension | LSBU | Top
This page was established in 2007 and last updated by Martin Chaplin on 22 August, 2022