
Water dissociation
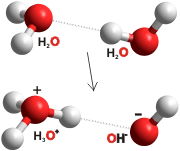
A remarkable property of pure water is that it dissociates to form hydrogen ions (H3O+) and hydroxide (OH−) ions.
![]() Variation in Kw with temperature and pressure
Variation in Kw with temperature and pressure
![]() Acidity, basicity, and the pKa of water
Acidity, basicity, and the pKa of water
![]() Weak acids
Weak acids
![]() Hydrogen ions
Hydrogen ions
![]() Hydroxide ions
Hydroxide ions
![]() Grotthuss mechanism
Grotthuss mechanism
![]() Ionic strength
Ionic strength
'I will employ the name “hydrogen ion exponent” and
the symbol pH for the numerical value of the exponent of this power'
Søren Sørensen, 1909
Water dissociation (autoionization; self-ionization) occurs endothermically d due to electric field fluctuations between neighboring molecules. Dipole librations [191], resulting from thermal effects and favorable localized hydrogen bonding [567], together with nuclear quantum effects [2025, 4456], cause these fluctuations. The process may be facilitated by exciting the O-H stretch overtone vibration [393]. Once formed (at an average concentration of about 1 M H2O-H+···OH− at femtosecond timescales, as reported by Vasily Artemov's group [1984]),h the ions may separate through the Grotthuss mechanism. Usually (>99.9%), these ion-clusters rapidly recombine (≈ 20 ps [2171]) with a frequency in the terahertz range to give the long-lived ions conventionally found. Thus the exact hydrogen ion concentrations depend on the time scale at which these are probed. Rarely (about once every eleven hours per molecule at 25 °C, or less than once a week at 0 °C), the localized hydrogen bonding arrangement breaks before allowing the separated ions to return [191]. The pair of ions (H+, OH−)g hydrate independently and continue their separate existencea for about 70 μs (this lifetimeis also dependent on the extent of hydrogen bonding, being shorter at lower temperatures). They tend to recombine when separated by only one or two water molecules.
H2O ![]() H+ + OH−
H+ + OH−
Kw = [H+] ˣ [OH−]
The kinetics of the process has been described using the equations, [4481]
![]()
The recombination (kr2) is assumed to be controlled by diffusion ( 0.112 M−1 ˣ ps−1), kd2 ≫kd1., and kr1 ≫kr2 , (kd1 =0.076 ˣ s−1, kr1 = 3.142 ˣ ps−1. The dissociation rate (kd2) was estimated at 2.04 ˣ 10−5 ˣ s−1 . The paired ions were found to be ion pairs separated by two water molecules (0.58 nm).
pKw is a dimensionless number (= 13.995, 25 °C [IAPWS]) as the included concentrations are relative to the molal standard states (e.g., 1 mol ˣ Kg−1). n This low occurrence of the ions means that at neutrality (pH 7, at 25 °C) c, similarly charged ions are, on average, separated by vast distances (≈ 0.255 μm) in molecular terms and (for example) bacteria contain only a few tens of free hydrogen ions (~ 30 in an Escherichia coli). Contributing to this effect is the high dielectric constant (encouraging charge separation) and high concentration of H2O (≈ 55.5 M; increasing the absolute amount dissociated). The mean lifetime of a hydroxonium ion (1 ps; about the same as that of a hydrogen bond) is such that the charge could be associated with over 107 molecules of water before neutralization.
Although the extent of dissociation is tiny ([H+]/[H2O] = 2.8 ˣ 10−9 at 37 °C), the dissociation and consequential changes in the tiny concentrations of hydrogen ions have absolute importance to living processes. Hydrogen and hydroxyl ions are produced already hydrated.
H2O (liq) ![]() H+(aq) + OH− (aq)
H+(aq) + OH− (aq)
where the subscripts, 'liq' and ‘aq’, indicate that the species are in or within the aqueous liquid phase.l
Hydration enthalpies of protons and hydroxides, from [1938b]
![Hydration enthalpies of protons and hydroxides, from [1938b] Hydration enthalpies of protons and hydroxides, from [1938b]](images/ionh2o.gif)
The protons (H+, hydrons) initially hydrate as hydroxonium ions, H3O+ (also called oxonium or hydronium ions) and do not exist as naked protons in the gas phase, or liquid, or solid water, where they interact extremely strongly with electron clouds. All three hydrogen atoms in the hydroxonium ion are held by strong covalent bonds and are equivalent (C3v symmetry in a vacuum). The thermodynamic properties of the dissociation at 25 °C and 0.1 MPa are ΔU° = 59.5 kJ ˣ mol−1, ΔV° = 22.13 cm3 ˣ mol−1, ΔH° = 55.8 kJ ˣ mol−1, ΔG° = 79.9 kJ ˣ mol−1, ΔS° = -80.8 J ˣ K−1 ˣ mol−1 [1938]. The proton is never found unhydrated in an aqueous solution, and the hydroxonium ions, H3O+, also have negligible independent existence in an aqueous environment [2134]. All the hydroxonium ion protons are predominantly hydrogen-bonded, causing further hydration to H3O+(H2O)n, where n depends on the conditions such as temperature, solutes, pressure, and method of determination. [H+] is often written instead of [H3O+].
To avoid the misleading presumption of the existence of bare protons similar to other bare cations (but see [2132] for an alternative view), the above equations are better written as:
2 H2O(aq) ![]() H3O+(aq) + OH−(aq)
H3O+(aq) + OH−(aq)
Kw = [H3O+] ˣ [OH−]
![]()
Change in volume on water dissociation, from [1946]
![Change in volume on water dissociation, data from [1946] Change in volume on water dissociation, data from [1946]](images/dvion.gif)
Both ions are ionic kosmotropes, hydrating and creating order in forming stronger hydrogen bonds with surrounding water molecules than the water molecules form between themselves and creating short chains of hydrogen-bonded water molecules [2025]. Remarkably, the volume change in this reaction
2 H2O(l) ![]() H3O+(aq) + OH−(aq) ΔV = -22.3 cm3 mol−1
H3O+(aq) + OH−(aq) ΔV = -22.3 cm3 mol−1
at 25 °C and infinite dilution, [1946], see Figure right,
due to the change in the hydration strength plus electrostriction, is about the same as one molecule of water (18.1 cm3 ˣ mol−1); when one water molecule ionizes, its volume effectively disappears.
The concentrations of H3O+ and OH− are normally taken as the total concentrations of all the singly charged small clusters including these species. As other water molecules are required to promote the hydrolysis, the equations below includes the most important. None of these hydrated ions should be considered as 'fixed' structures, with further water molecules continually coming and going in aqueous solution with timescales of picoseconds. No bare protons occur, however.
4 H2O ![]() H5O2+ + H3O2−
H5O2+ + H3O2−
10 H2O ![]() H13O6+ + H7O4−
H13O6+ + H7O4−
The concentration of hydroxonium and hydroxide ions produced is equal to the square root of the dissociation constant (Kw).
A wide range of values for Kw has been calculated using Quantum Cluster Equilibrium (QCE) theory with various ab initio and density functional methods [3025].
The reverse reaction
H3O+(aq) + OH−(aq) ![]() 2 H2O(aq) Keq = 1014
; 25 °C
2 H2O(aq) Keq = 1014
; 25 °C
greatly favors the neutralization reactions of acids and bases.
Aqueous OH− does not ionize further as (O2− + H2O ![]() 2 OH−,
K > 1022). H3O+ does not protonate further to the tetrahedral H4O2+ ion as although H4O2+ may be metastable in the gas phase, it is thermodynamically unstable to loss of a proton [2133], and would immediately dissociate in aqueous solution. [Back to Top
2 OH−,
K > 1022). H3O+ does not protonate further to the tetrahedral H4O2+ ion as although H4O2+ may be metastable in the gas phase, it is thermodynamically unstable to loss of a proton [2133], and would immediately dissociate in aqueous solution. [Back to Top ![]() ]
]
pH of common materials

The hydronium (oxonium) ion concentration (commonly called 'hydrogen ion concentration') is often given in terms of the pH, where
pH = Log10(1/[H3O+]) = -Log10([H3O+])
(that is, [H3O+] = 10−pH) f with the concentration of H3O+ in mol ˣ L−1. This equation is adequate for most solutions but may fail under higher solute concentrations.
More accurately and as determined using a pH meter,
pH = -Log10(aH) = -Log10(mH ˣ λH/m°)
where aH, mH, λH, and m° are the relative (molality based) activity, molality, molal activity coefficientj, and standard molality (1 mol ˣ [kg solvent]−1) of the hydrogen ions. This equation is correct under higher solute concentrations. Proof that the use of the equation pH = -Log10([H+]) may give misleading results (and pH = -Log10(aH) is preferred) is easily shown as the pH of 0.1 M HCl decreases (i.e., it apparently becomes more acidic) when it is diluted with 5% M LiCl [1107]. Also, the -Log10([H3O+]) for average seawater at 25 °C is 8.19, but its -Log10(aH) is 8.32. As pH involves activities, the [H3O+] calculated from pH = -Log10([H+]) is often not the [H3O+] concentration experimentally determined by titration. The hydrogen ion activity cannot be evaluated thermodynamically [3376] but may be determined kinetically.
Water can thus support acid-base equilibria over a range of about 16 pH units (see above right). At the low concentrations usually found, the molarity-based hydrogen ion concentration is close enough to the relative (molality based) activity for its use in most circumstances. The presence of salts and other solutes will generally reduce this activity, and the activity varies with temperature. The molal activity of hydrogen ions cannot be determined directly but may be determined using a glass electrode standardized to the response of standard buffer solutions of comparable ionic strength. o Glass electrode-determined pH values are error-prone, and calculated hydrogen ion concentrations should be treated with caution, particularly at the extremes of pH [1890]. For more information and a list of primary pH standards, see [813].
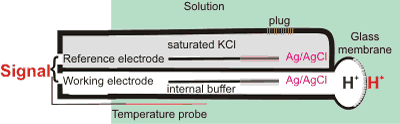
The pH scale was first introduced by Sørensen (as pH·) in 1909 [1036] using colorimetric measurements and the hydrogen electrode, which generates an electrode potential proportional to pH. Today, we commonly use the glass electrode [3377] (see right), which also gives an electrode potential dependent on the activity of the H+and proportional to pH in dilute solution,
![]()
where F, R, and T are the Faraday constant, the gas constant, and absolute temperature, respectively. E refers to the potential (V) of the “unknown” solution being determined, and ES and pHS refer to the standard reference electrode solution. Once calibrated with a solution of Known pH
pH ∝ E
with a proportionality correction being applied for the temperature. The pH's are reasonably accurate where the pH meter is calibrated close to the pH at issue and with a solution of approximately the same ionic strength [3378].
The pH meter can be used to estimate hydrogen ion concentrations without concern for knowing activities [3376]. pH electrodes are now commonly used to determine the pH (see right).i The pH scale extends to negative numbers (for example, concentrated HCl has a pH of about -1.1) and to greater than 14 (for example, saturated NaOH has a pH of about 15.0) [1187]; although the glass electrode cannot be used at such extreme pH's. There is a review of the pH of natural water [1712].
Similarly to pH, pKw is defined by
pKw = Log10(1/Kw) = -Log10(Kw)
utilizing concentrations in mol ˣ L−1.
Where the solution contains significant amounts of heavy water (D2O), the measured pH will differ slightly from that expected from the sum of the amounts of the protonated species H3O+ + H2DO+ + HD2O+ + D3O+ [2953].
[Back to Top ![]() ]
]
pKw versus temperature
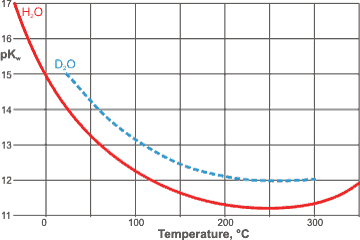
Kw is very temperature dependent, increasing with temperature (that is, from 0.001 ˣ 10−14 mol2 ˣ L−2 at -35 °C (pH 8.5) [112], 0.112 ˣ 10−14 mol2 ˣ L−2 at 0 °C (pH 7.5), to 0.991 ˣ 10−14 mol2 ˣ L−2 at 25 °C (pH 7.0), to 9.311 ˣ 10−14 ˣ mol2 ˣ L−2 at 60 °C (pH 6.5) [87]), to 10−12 ˣ mol2 ˣ L−2 at 300 °C (pH 6.0, ≈ 50 MPa) [456] in agreement with the high positive standard free energy. b There is a minimum at about 249 °C along the saturated pressure line for H2O and at about 257 °C for D2O (see right [1865]). The pKw H2O minimum is about 0.74 lower than that for D2O [1865]. (see also conductivity maximum).
A theoretical treatment of this temperature dependence is available [763].
Variation in pKw ( pKa)
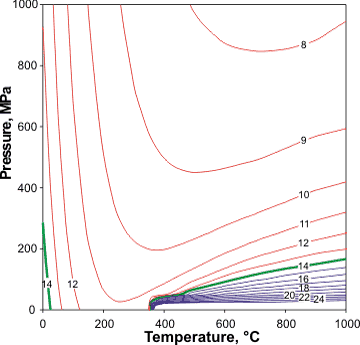
pKw versus pressure
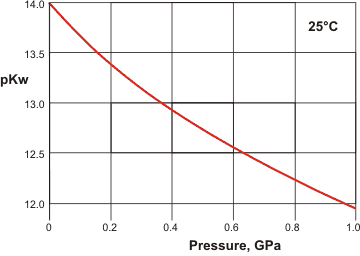
Temperature and density dependence of dissociation have been examined [1321]. Dissociation depends on the pressure, with Kw doubling at about 100 MPa; unsurprising given the negative ΔV associated with the dissociation, -18.1 cm3 ˣ mol−1.
pKw versus water density, changing T and P
towards and past critical point, from [4121]
![pKw versus water density from [4121] pKw versus water density from [4121]](images/pkw-dens.gif)
Using the different methodology of direct, conductivity measurements, the results from the University of Guelph [4121] show discrepancies from these values between 350 °C, and 401 °C, and between 5.75 MPa and 31.15 MPa, which reach between two and five orders of magnitude near the critical point.
The actual pKw of solutions is rarely 14.0 [4245] as dissociation also varies with solute concentration and ionic strength; for example, Kw goes through a maximum of about 2 ˣ 10−14 mol2 ˣ L−2 (minimum pKw ~13.7) at about 0.25 M ionic strength (using tetramethylammonium chloride, where possibly the change in hydrogen-bonding caused by clathrate formation encourages dissociation) before dropping to a value of about 1 ˣ 10−16 mol2 ˣ L−2at 5 M (with higher concentrations disrupting the hydrogen-bonding). Similar maxima occur with other salts such as NaCl (≈ 0.6 M), KCl (≈ 0.45 M), KNO3 (≈ 0.5 M) and NaClO4 (≈ 0.5 M) [2234]. Dissociation will also be different at interfaces; for example, it is greater at lipid membrane surfaces [1964].
In ice, where the local hydrogen-bonding rarely breaks to
separate the continually forming and re-associating ions, the
dissociation constant is much lower (for example, at -4 °C, Kw = 2 x 10−20 mol2 ˣ L−2 ). [Back to Top ![]() ]
]
There has been controversy and confusion for the last 90 years over the aciditye of water and its pKa; a confusion that is yet to be fully clarified. Does the pKa of H2O equal 15.74 [2966] or 14.00 [2965]? The answer depends on the standard state used for the solvent water.m
The acidity constant (Ka) of weak acid HA,k
HA (aq)+ H2O (l)![]() A− (aq) + H3O+(aq) ΔG°
A− (aq) + H3O+(aq) ΔG°
where HA is an acid having its conjugate base A−; also H2O is acting as a base with its conjugate acid H3O+
Ka is defined by
Ka= [H3O+][A−]/[HA]
pKa= -Log10(Ka)
therefore,
ΔG° = - RT Ln( Ka)
pKa= ΔG°/(ln(10) ˣ RT)
Together with its conjugate base A−, we get,
HA (aq) + H2O (l) ![]() A− (aq)+ H3O+ (aq) ΔGa° = - RT Ln( Ka)
A− (aq)+ H3O+ (aq) ΔGa° = - RT Ln( Ka)
A− (aq)+ H2O (l) ![]() HA (aq) + OH− (aq) ΔGb° = - RT Ln( Kb)
HA (aq) + OH− (aq) ΔGb° = - RT Ln( Kb)
_________________________________________________________
H2O (l) + H2O (l) ![]() H3O+(aq) + OH− (aq) ΔGw° = - RT Ln( Kw) = 79.89 kJ ˣ mol−1 [2967]
H3O+(aq) + OH− (aq) ΔGw° = - RT Ln( Kw) = 79.89 kJ ˣ mol−1 [2967]
Where the ΔG° values are the standard Gibbs free energies for the equilibria.
Therefore, as ΔGw° = ΔGa° + ΔGb°, Ln( Kw) = Ln( Ka) + Ln( Kb) and
pKa+ pKb = pKw and Kw = Ka ˣ Kb
H2O, as a weak acid, may be treated in the same way
H2O (l) + H2O (l)![]() H3O+(aq) + OH− (aq)
H3O+(aq) + OH− (aq)
Its pKa has been (mistakenly) derived as
Ka= [H3O+][OH−]/[H2O] = Kw/[H2O] = Kw/55.345 (at 25 °C)
and pKa = pKw +1.743 (= 15.738 at 25 °C)
However, in this derivation, the H2O is treated both as an acid ([H2O] in the denominator, equaling about 55.345 mol ˣ L−1), and the solvent (internalized in the Ka definition with a value of unity). This disparity in values introduces conflict.
The alternative (and correct) derivation utilizes the activity of water (equals unity) in the denominator [1321, 2965]
Ka (H2O)= [H3O+][OH−] = Kw = 10−13.995 (a number without units)
pKa = pKw = 13.995 (H2O, 25 °C)
H2O is a very weak acid; compare with the pKas of H2Te, H2Se, and H2S that are 2.6, 3.89, and 7.04, respectively. The pKb (= pKw - pKa = 0.00) related to this Ka concerns the conjugate base (OH−), and not H2O, as commonly mistakenly cited. OH− is a strong base, whereas H2O is a very weak base. The pKb of H2O is derived exactly as pKa (above, as the equation generates both an acid and a base) and gives the same value (= 13.995 at 25 °C).
Although a true ionization constant is a thermodynamic quantity related to the standard free energy change and should be independent of the concentration used for its determination, in practice, it will vary (a little) with this concentration due to interactions between the ions (i.e, their activities).
H3O+ is a strong acid with associated Ka (H3O+) equaling unity exactly (see the equation below). pKa (H3O+) equals zero exactly and is invariant with temperature, as ΔG° is necessarily zero.
H3O+(aq) + H2O (l) ![]() H2O (l) + H3O+(aq) ΔG° = - RT Ln(Ka (H3O+)) = 0.00 kJ ˣ mol−1 [2967]
H2O (l) + H3O+(aq) ΔG° = - RT Ln(Ka (H3O+)) = 0.00 kJ ˣ mol−1 [2967]
There is a difficulty that has been ignored in these definitions as Ka and Kb would normally be expressed in terms of activities rather than concentrations [1188], and the activity of pure H2O is defined as unity, whereas that of solutes is defined relative to their standard state (1 mol ˣ kg−1) rather than the concentration of water (≈ 55.345 mol ˣ L−1). It is essential that the chosen value (pKa = 13.995 for H2O) fits in with the known acidity and basicity of water compared with other materials. While older published materials reported methanol as being more acidic (pKa = 15.3) than water [2107] (and so mistakenly favoring a pKa for water of 15.74), a re-analysis [2965] shows that water is 35-fold more acidic than methanol. This value fits well with the pKa of H2O being ≈ 14. This value (pKa = 14.00) may be separately determined from thermodynamic ΔG data [2967].
Where weak acids with similar pKas are adjacent (and therefore the pKa values of the H-bond donor and acceptor groups are nearly equal), they may form low-barrier hydrogen bonds with easy exchange of the proton' for example,
CH3COOH + C2H5COO− ![]() CH3COO− + C2H5COOH
CH3COO− + C2H5COOH
[Back to Top ![]() ]
]
a It follows that pure water droplets containing less than about 108 water molecules (≈ 0.1 μm radius) would usually (i.e., on average) contain no ions in the absence of surface effects. [Back]
b A bulk energy diagram for the dissociation in bulk water has been described [604]. [Back]
c Note that acid-base neutrality only occurs when the concentration of hydrogen ions equals the concentration of hydroxyl ions (whatever the pH). This only occurs at pH 7 in pure water when at 25 °C. A solution is acidic when the hydrogen ion concentration is greater than the hydroxide ion concentration, whatever the pH. The pH of a neutral solution is numerically equal to half the pKw of the solution. Therefore a pH of 7 at 0 °C indicates a slightly acid solution (neutrality is pH 7.5), whereas a pH of 7 at 50 °C indicates a slightly alkaline solution (neutrality is pH 6.6). [Back]
d In a vacuum the reaction
H2O (g) ![]() H+ (g) + OH− (g)
H+ (g) + OH− (g)
requires over three times more energy (1.66 MJ mol−1; Kw = 1 ˣ 10−285 mol2 ˣ L−2 [3025]) than dissociation
H2O (g) ![]() H· (g) + ·OH (g)
H· (g) + ·OH (g)
(531 kJ ˣ mol−1). In liquid water, the hydration of the ions (H+ ΔG° hydration -1112.5 kJ ˣ mol−1, this includes H3O+ ΔG° hydration -461.1 kJ ˣ mol−1; OH− ΔG° hydration -437.6 kJ ˣ mol−1 [1067]) reduces the ΔG° of the reaction
2 H2O (l) ![]() H3O+ (aq) + OH− (aq)
H3O+ (aq) + OH− (aq)
to +99.78 kJ ˣ mol−1 (These calculations assume that the standard state of the solvent water is taken as 1.0 M. If the standard state of the solvent water is the unit activity or mole fraction (= 1.0), the ΔG° is +79.907 kJ ˣ mol−1 as given above). The dissociated radicals (H·, ·OH) are also somewhat stabilized in liquid water, as shown by the occasional dissociation of water [1066, see equations]. [Back]
e Note that the 'acidity' of a material is commonly its pH and depends both on its pKa and its concentration. The 'acidity' of drinks and foodstuffs, however, also depends on the response of our taste buds. [Back]
f As Logarithms may only be taken of dimensionless numbers, all the concentrations (activities, partial pressures, etc.) in any Logarithmic expression are actually divided by unit values in the same units of that concentration (activity, partial pressure, etc.); thus, for example, here [H3O+] (concentration of H3O+ in mol ˣ L−1) is actually [H3O+]/(1.0 mol ˣ L−1).
The p in pH originated as the arbitrary choice for the naming of the electrode solutions 'p' and 'q' by Sørensen [1036, 1891], but is now taken to mean the 'logarithm to the base 10 of the reciprocal of' (cologarithm) as in the function described above. [Back]
g Strictly speaking, these equations should be expressed in terms of activities rather than concentrations; thus
Kw = [aH+] ˣ [aOH−]
The derivations are easier to follow as given, and usually the concentrations are so small that the difference is inconsequential. [Back]
h Similar concentrations are found for ice [2171]. [Back]
i Different membrane glasses may be used dependent on the solution to be analyzed (e.g., high temperatures, strong alkali or HF).
The electrode reaction for the Ag/AgCl/saturated KCl reference electrode is
AgCl + e− ![]() Ag0 + Cl− E = +0.197 V (in saturated KCl)
Ag0 + Cl− E = +0.197 V (in saturated KCl)
[Back]
j The activity coefficient of hydrogen ions depends on the acid concentration, temperature, ionic strength, the dielectric constant, the size of the ions, and the density of the medium. [Back]
Titration curve of a weak acid with pKa = 7
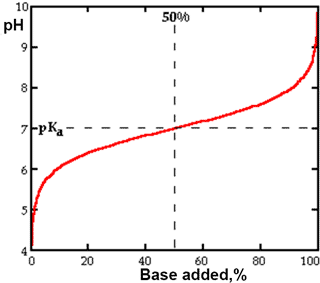
k Weak acids A weak acid is only partially dissociated, with both the undissociated acid and its dissociation product(s) being present, in solution, and in equilibrium with each other. The dissociation constant (Ka) may be determined by titration (see right).
If we consider the situation where the acid is one half dissociated, in other words where [A−] is equal to [HA], then the solution's pH equals the acid's pKa. This means that an acid is half dissociated when the pH of the solution is numerically equal to the pKa of the acid. Therefore acids with the lowest pKa values are able to dissociate in solutions of low pH, i.e., even where the hydrogen ion concentration is high. Acids with higher pKa values dissociate only in solutions of high (more alkaline) pH. The pKa values of carboxylic acids are examined elsewhere as are those associated with CO2. A compilation of weak acid pKa values is available.
For any weak monoprotic acid (HA) of concentration c, the equilibrium is,
HA ![]() [H+] + [A−]
[H+] + [A−]
The concentration of hydrogen ions [H+] is given by the following four equations,
Ka= [H+] ˣ [A−]/[HA]
Kw = [H+] ˣ [OH−]
Balancing charges
[H+] = [OH−] + [A−]
Mass balance of the acid
c = [A−] + [HA]
Eliminating [A−], [HA] and [OH−] gives
[H+]3 + Ka ˣ [H+]2 − (Ka ˣ c + Kw) ˣ [H+] − Ka ˣ Kw = 0 (A)
The pH is,
![]()
Comparison of actual pH with its approximation for acetic acid
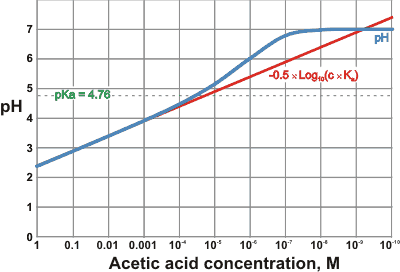
so long as c ≫ Ka and c ˣ Ka > Kw.
The pH, calculated using a numerical iterative method from the above exact equation (A), is compared with its approximation -0.5 ˣ Log10(c ˣ Ka) for acetic acid (pKa = 4.76, 25 °C) is shown on the right.
It can be seen that the approximation should not be used for concentrations below about 0.1 ˣ Ka. At very low acid concentrations (< 10−7 M), the pH cannot rise above pH 7.0.
An extremely useful relationship between pH and pKa can be obtained simply by taking logarithms of
Ka= [H+] ˣ [A−]/[HA]
log10(Ka) = log10[H+] + log10([A−]/[HA])
as pKa = -log10(Ka) and pH = -log10[H+], this gives the Henderson-Hasselbalch equation,
![pH=pKa+log([A-]/[HA]) pH=pKa+log([A-]/[HA])](images/hheq.gif)
This equation may break down at high (> 1 M) and low (< 1 mM) concentrations and where the pH is more than two units distant from the pKa.
The most convenient form of this Henderson-Hasselbalch equation is
![]()
Using pKa values, one can express the strength of an acid (i.e., its tendency to dissociate) with reference to the pH scale. A weak acid only slightly dissociates in solution and has a low Ka and high pKa.
A strong acid is mostly, perhaps wholly, dissociated and therefore has a high Ka value and a low, perhaps even negative, pKa value. If the Ka is large, then pKa will have a small (or negative) numerical value. There is no generally accepted dividing line between weak and strong acids, but as a rough guide, it is suggested that a strong acid would be at least 25% dissociated in a 0.1 M solution; this correspondis to a Ka of about 0.01 (pKa ~2). It has been found that the strong acids HCl, HBr, and HI are 91%, 95%, and 99 % dissociated, respectively [3505] (see also elsewhere). At high concentrations ( > ~0.1 M), the activities of the ions and water deviate increasingly from unity, and the pH is best experimentally determined.
Strong bases remove protons from molecules of acid, including even a very weak acid, and they also dissociate fully in water. Examples are the hydroxides of the alkali metal ions, e.g., LiOH, NaOH, and KOH.
pKa values are used both for acids and for the conjugate acids of bases. Thus NH3 has pKa for the dissociation
NH4+ ![]() H+ + NH3
H+ + NH3
of about 9.3.
[Back]
l Auto-ionization is not restricted to water but can occur with a few other substances. An example is liquid ammonia with ionization equilibrium
NH3 + NH3 ![]() NH2−(in NH3) + NH4+(in NH3)
NH2−(in NH3) + NH4+(in NH3)
KNH3= [NH4+][NH2−]
The self-ionization constant (KNH3) of ammonia (at ≈ 10−30) is sixteen orders of magnitude smaller than that of water. [Back]
m Water pKa has been calculated using first-principles to a value 1.0 units different from the experimental value [3839]. [Back]
n Some reports give this unit as 1 mol ˣ L−1. [Back]
o Ionic strength. The ionic strength of a solution is a measure of its ionic concentration. The ionic strength (I, mol ˣ L−1) of a solution is defined (empirically) as,
![]()
where the factor of ½ is to include both cations and anions, ci is the molar concentration of ion i (mol ˣ L−1), zi is the charge on that ion, and the sum is taken over all ions in the solution. The term was introduced by G. N. Lewis and M. Randal in 1921 (G. N. Lewis and M. Randall, The activity coefficient of strong electrolytes, Journal of the American Chemical Society, 43 (1921) 1112-1154). For a 1:1 electrolyte such as sodium chloride, where each ion is singly-charged, the ionic strength is equal to the concentration (c). For a 1:2 electrolyte such as magnesium chloride, the ionic strength is equal to three times the concentration of the salt as
I = 0.5 ˣ {c ˣ (−1)2 + c ˣ (−1)2 + c ˣ (+2)2} = 3 ˣ c
The ionic strength of the solution reflects its charge density. It affects many properties, such as the solubility and dissociation of its ionic components and the activity and solubility of contained biological molecules. As the usefulness of the concept of 'activity' diminishes with the increased understanding of the molecular structuring of water by itself and surrounding solutes, the concept of 'ionic strength still retains its usefulness in such areas as the control of biological processes.
As volumes of solutions are not generally additive, it may be useful to use the molal ionic strength, where all the concentrations are in molalities (as in its original definition). [Back]
Home | Site Index | The water molecule | Hydrogen ions | Hydroxide ions | Grotthuss mechanism | Hydrogen bond | LSBU | Top
This page was established in 2000 and last updated by Martin Chaplin on 24 August, 2022