
Yellowstone fumarole
showing condensed liquid water droplets

![]() Water dimer and small clusters
Water dimer and small clusters
![]() Airborne water
Airborne water
![]() The Leidenfrost effect
The Leidenfrost effect
![]() Hexagonally-patterned microdroplets
Hexagonally-patterned microdroplets
![]() Ideal gas
Ideal gas
Water vapor is an odorless, transparent, invisible gas that exists in the air over a wide range of temperatures and pressures. What is commonly known as steam (see right) are condensed liquid water droplets suspended in the air (i.e., an aerosol of colloidal particles similar to those carbon particles occurring in smoke). Water vapor in the atmosphere condenses into clouds of tiny liquid droplets that scatter light and may precipitate. Water has a very low vapor pressure for its molecular weight and so does not boil until the relatively high temperature of 100 °C at 101.325 kPa. It takes much energy to boil and increases its volume by 1700 times. Most of the water vapor in the air is derived from evaporation from the sea, mainly tropical seas, with an Equation of State for Humid Air in Contact with Seawater described [4268]. Surface temperature and wind speeds play key roles. The water vapor saturation over ice is less than over a water surface at the same temperature.
At sufficiently high temperatures or low pressures all particles in a gas phase obey the Ideal Gas Lawd where no forces are exerted between the gas particles.
PV = nRT = n ˣ NA ˣ kB ˣ T
where P, V, T, and n are respectively the pressure (Pa), volume (m3), temperature (K), and the amount of the gas (mol), R is the ideal gas constant (J ˣ mol−1 ˣ K−1), NA is the Avogadro number and kB is the Boltzmann constant. The Ideal Gas Law does not hold exactly at higher pressures or lower temperatures when the finite size of the particles, and the interactions between particles have significant effects. The empirical equation below (the van der Waals equation) then fits better,
(P + n2a/V2) ˣ (V - nb) = nRT
where a and b have partial theoretical bases on the reduced pressure due to the attractions of the molecules to each other (a; and proportional to the density) and the size of the molecules (b; the volume of the particles detracting from the total volume)), respectively. The theoretical bases are not exact and both (a) and (b) may vary with the temperature and density.
Gaseous water is water vapor and one of the lightest of gases. In science and engineering, the word 'steam' is also used for water vapor (i.e., gaseous water), but usually when above the boiling point of water. As commonly used in the English language, 'steam' also may mean the white cloud of fine liquid water droplets of condensed water vapor produced by a boiling kettle or fumaroles (see top right). When water is heated in a pan, air molecules are driven out of the solution and gather crevices on the pan's surface. These air bubbles grow and are released until most atmospheric molecules are released. This bubbling indicates that the water is heating but does not indicate that steam is formed. Boiling is initiated at about 100 °C, at normal atmospheric pressure, by the formation of small vapor-filled voids which increase in size, merge, and produce gaseous bubbles containing water molecules (steam). Initially, these are at higher than atmospheric pressure. Then, the pressure reduces, and these bubbles collapse in the cooler water as they rise, making a popping noise. When the water is hot, these bubbles grow and rise before bursting at the liquid's surface to give steam. Further heating results in a lesser popping noise as most of the bubbles reach the surface and the water is fully boiling. Evaporation is different from boiling as it only occurs at the surface of the liquids, whereas boiling can occur throughout the liquid. Boiling water for a minute kills most microorganisms and viruses.
Water vapor is transparent to 'visible' light but absorbs strongly in the infrared. It is the main absorber of the sunlight in the atmosphere; without it, the Earth would be in a permanent ice age. The mechanisms through which water vapor in the lower troposphere (at temperatures up to around the triple point of water; ≈ 0.01 °C, ≈ 5 km) influences convection, circulation and the formation of clouds, have been reviewed [3139].
The 13 trillion tons of water in the atmosphere (≈ 0.33% by weight) is responsible for about 70% of all atmospheric absorption of radiation, mainly in the infrared region where water shows strong absorption. Atmospheric water contributes substantially to the greenhouse effect, more than twice that of carbon dioxide, ensuring a warm habitable planet, but operates a negative feedback effect due to cloud formation reflecting the sunlight away. Molecular rotations and vibrations are obtained using the spectroscopic data and summarized for all water's isotopologues by IUPAC [3035].
As with other gases, gaseous water is not an ideal gas, although it behaves nearly as an ideal gas at low densities, approximately obeying the relationship (the equation of state, EoS),
P = r ˣ R ˣ T
P = kB ˣ T/V
where P is the pressure ( Pa), r is the molar density (mol ˣ m−3 ), R is the gas constant (J ˣ mol−1 ˣ K−1), T is the temperature (K), kB is the Boltzmann constant, and V is the volume (m3) of a mole of the molecules (mol ˣ NA).
At higher densities, corrections can be applied
P/rRT= 1 + Br + Cr2 + Dr3 +...
P = kB ˣ T ˣ (1/V + B2(T)/ V2 + ...
where B2(T) is negative at low temperatures and positive at high temperatures. At B2(T) = 0, attractive and repulsive forces are balanced, as in an ideal gas [3853].
Variation of the second virial coefficient, from [3034]
![Variation of the second virial coefficient with temperature, from [3034] Variation of the second virial coefficient with temperature, from [3034]](images/virial.gif)
The second virial coefficient (B) depends on temperature. Except at high densities, the higher virial coefficients (C, D, etc.,) are usually ignored (i.e., they are put equal to zero). It can be seen right that the second virial coefficient increases considerably at lower temperatures [3034]. This indicates more significant deviations from ideal behavior at lower temperatures partially due to dimer formation (shown blue right [3037]). The data for D20 is also shown as dotted lines with only limited data available for D20 second virial coefficient [3038].
Hydrogen-bonding between water molecules occurs in the gas phase with, typically within the ambient atmosphere, over one water dimer forming for every thousand free water molecules rising to about one in twenty in steam. The dimer formation, and the order it brings are a major cause for the large deviations from ideal gas behavior in gaseous water and are particularly relevant at higher pressures.
The thermodynamic properties of gaseous water above 100 °C, 101,325 Pa, are described by The International Association for the Properties of Water and Steam (IAPWS). Another analytical representation of the ideal-gas Gibbs free energy for water has been developed based on the molecular structure of water and using just six molecular constants [4280]. Experimental data for dilute gas-phase heavy water (D2O) are available for viscosity and thermal conductivity and have been calculated for molecular diffusion [3036]. The thermodynamic properties of gaseous water below 100 °C, supersaturated (supercooled) steam at conditions occurring in steam turbines have been studied by several theoretical and semi-theoretical methods [3507].
The maximum amount of water in the air, at 1 atm
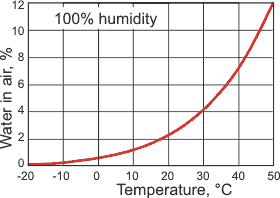
Water is present in the atmosphere in both liquid and gaseous forms. The maximum gaseous composition depends on the atmospheric temperature (see right). The average relative humidity of the atmosphere is about 75% at ground level, reducing to about 45% at 5000 m.
The semi-empirical Antoine equation gives the saturated vapor pressure of water in the air,c
Log10(P) = A − {B/(T + C)}
where P is the saturated vapor pressure of water in Pa and K is the temperature in kelvin (256 - 373 K); the empirical constants A, B, and C are 9.6543, 1435.264, and -64.848, respectively.b The experimental vapor pressure at 25 °C is 3.165 kPa (calculated = 3.179 kPa). The density of 'moist' air is always lighter than 'dry' air at the same temperature and pressure, as the molar mass of dry air is 28.57 g ˣ mol−1 (0.9461 kg ˣ m−3 at 100 °C, 101.325 kPa, [540]) compared with water vapor of 18.02 g ˣ mol−1 (0.5976 kg ˣ m−3 at 100 °C, 101.325 kPa).
The fugacity of water is described elsewhere.
When we breathe out, we may exhale moist air, e visible water droplets, and an aerosol of invisible (nm - µ+ radius) water droplets. This water vapor increases the humidity of the air. This aerosol might not be visible but may be detected by a water-cluster-detecting breath sensor developed for detecting drunk or drowsy drivers [1801]. Aerosol droplets can also be produced by flushing a toilet. These respiratory droplets, produced by talking, coughing, and sneezing, may contain viral, fungal, and bacterial pathogens, and transmit infectious diseases, such as influenza, COVID-19, colds (adenoviruses, rhinoviruses), pneumonia, tonsillitis, scarlet fever, and meningitis [4134a]. Normal talking may produce over 100 particles per second (containing 105 - 108 virus particles per milliliter), some of which remain airborne for several minutes. As the sedimentation time is inversely proportional to the square of the droplet size, in the absence of evaporation, a 200 µm diameter droplet drops at 1 m ˣ s−1 whereas a 2 µm diameter droplet drops at 0.1 mm ˣ s−1. These drop velocities are much smaller if evaporation is taken into account, which is more important at lower relative humidity.
Just a few individuals may disseminate and disperse the majority of infectious particles. Tiny droplets (< 5 µm including nanodroplets produced in building ventilation, air conditioners, cruise liners, and aircraft, for example) may stay air-bound for over a week. Indoors, even large droplets (up to 100 µm) may stay air-bound for much longer periods due to the restricted (sometimes upwards) indoor air circulation and, even if they fall, they may become airborne again once they dry out (desiccate) or land on touchable surfaces, like doorknobs, buttons, and tabletops. Whether infected droplets remain infectious depends on the environment, the infectious dose, and the pathogen. Virus survival depends on the temperature with low temperatures (e.g., ~8 °C), giving the greatest viral survival. Generally, bacteria are more resistant to higher temperatures than viruses. Influenza is most transmissible (infectious) under cold, dry conditions with high humidity leading to its inactivation after coughing [4159].
Even though there are more colds and flu, etc., in the cold season (winter in the northern hemisphere), there does not seem to be a strong connection of the pathogen spread to temperature; despite this strong correlation. In winter, heating the buildings, particularly central heating, dries the cold air coming in from outside, causing the relative humidity to drop. However, relative humidity affects the stability of viruses in aerosols. Heating the buildings in winter, particularly central heating, dries the cold air coming in from outside, causing the relative humidity to drop. The presence of the occupants may not be sufficient to raise the indoor humidity [4137]. As a result, indoor relative humidity in temperate regions typically varies between 10% and 40% in the winter months, which is significantly lower compared with its range of 40% to 60% in the summer months [4134b]. For example, if air enters at 10 °C and 70% relative humidity and is warmed to 20 °C, its relative humidity drops to 37%. The stability and infectivity of winter viruses trapped in those droplets show a striking correlation with low relative humidity. At low relative humidity, the droplets dry out to leave the pathogens suspended for much longer within much smaller droplets in the air. Also, dry air dries out the mucous membranes in the nose, which eases the invasion of infectious viruses into the respiratory tract. Subjects with a natural tendency to dry respiratory mucosa are particularly vulnerable to the Covid-19 virus, as the mucous membranes of the upper respiratory tract are required to present the first essential barrier against Covid-19 virus infection. Also, dry respiratory mucosa correlates with age, leaving the elderly more prone to infection. Further, dry nasal mucosa correlates with loss of smell and taste [4138], and loss of smell and taste are indicative of Covid-19 infection.
The improved stability (and infectivity) of SARS coronavirus at low temperatures and low humidity environments has been reported to facilitate its transmission in subtropical areas (such as Hong Kong and Guangzhou) during the spring and within air-conditioned environments. It may also explain why some Asian countries in tropical areas (such as Malaysia, Indonesia, or Thailand) with high temperatures and high relative humidity environments did not have major community outbreaks of SARS [4135a]. Similar findings, from 166 countries, provide evidence that the COVID-19 pandemic may be partially suppressed with humidity increases [4135b]. Within our housing, air humidity negatively correlates with Covid-19 morbidity and mortality [4137].
[Back to Top ![]() ]
]
The Leidenfrost effect
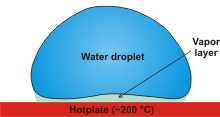
An interesting effect (the Leidenfrost effect, a [2291, 2771, 3649, 4319] see right) is that liquid water
droplets remain far longer on a hot plate (up to 5000 times as long) just above 200 °C
than if the hot plate was just above 100 °C. The temperature at which this (the temperature boundary between the surfacel-iquid heating and film boiling regimes) occurs depends on the surface material and its roughness (and the liquid involved as the Leidenfrost effect is a general one for all liquids) [4425]. Once formed, the droplets move around the surface in a rapid motion. See [960]
for an amusing scientific answer to how water boils. The Leidenfrost effect is not superheating but due to the formation of an insulating vapor layer keeping that liquid from boiling rapidly. The water droplet's temperatures remain at about 90 °C when the plate is held at about 300 °C. For drop radii of
a few millimeters, the vapor thickness is about 100 μm. During the final stage of evaporation, the droplet takes off from the surface., unless any surface contamination bridges the vapor layer and causes it to explode [4428]
Evaporation times for 1 mm radius water droplet,
on a Duralumin plate, from [4426]
![Evaporation times for 1 mm radius water droplet, from [4426] Evaporation times for 1 mm radius water droplet, from [4426]](images/leidenfrost2.gif)
The droplet's rapid motion arises from an asymmetry in the vapor profile [3485]. If the hotplate surface is made superhydrophobic, the droplets remain even at lower temperatures (down to 22 °C) [1926]. On heated, curved surfaces, larger quantities of fluid, not just droplets, can be suspended [1957]. If placed in an electric field, Leidenfrost droplets jump from the hot surface higher and higher [2881]. The Leidenfrost effect has been used in nano-synthetic reactions to enable faster reaction rates. They may also be involved in sphere-in-cavity structures with residual drag coefficients less than 10% of solid objects of similar dimensions [3118].
A similar effect (the three-phase Leidenfrost effect) occurs with solid water (hexagonal ice) on a heated surface. However, this takes place at a much higher temperature [4419]. Both liquid and vapor film layers are found under the levitating ice. As this Leidenfrost effect does not start until the temperature is raised above 550 °C (on smooth aluminum), there is much better heat transfer than liquid water at lower temperatures (150 °C - 550 °C).
Another triple Leidenfrost effect has been described where drops of different liquids collide above a hot plate, bouncing several times before finally coalescing [4420]. The drops are not only in a Leidenfrost state with respect to the hot surface, but they also experience a Leidenfrost effect between them at the moment of collision.
There is an inverse Leidenfrost effect where hotter droplets (at room temperature) levitate above a very cold liquid, such as liquid nitrogen, at −196 °C [4427]. In this case, the droplets cause the cold liquid to evaporate by creating the repulsive cushion of vapor.
[Back to Top ![]() ]
]
Hexagonally-patterned microdroplets,
from [3331]
![Hexagonally-patterned microdroplets, from [3331] Hexagonally-patterned microdroplets, from [3331]](images/drop6.gif)
Self-organized hexagonally-patterned microdroplets (≈ 10 µm - 50 µm diameter) clusters have been found floating, as a single sheet, a dozen or so micrometers above locally-heated water (and other hydrogen-bonded liquids') surfaces [3331]. These flat levitating clusters of self-assembled ordered spherical droplets (see right) are formed by condensation of vapor above the locally (infrared or laser irradiated) heated water surfaces. They can be formed even at maximum surface temperatures as low as 27.6 °C. They are separated from each other and levitated above the liquid surface by about the droplet diameters. Their levitation is due to the dynamic balance between the evaporation and condensation balance for both water in the droplets and for the steam-air gas mixture around the droplets. Their organized array is due to the minimization of the entropy of the arrangement. The collapse of one droplet causes the collapse of all the droplets. Infrared irradiation of a droplet cluster prevents the coalescence of the cluster [3961]. Others have found that the droplets may demonstrate 4-fold, 5-fold, and 7-fold symmetry [4236].
[Back to Top ![]() ]
]
a J. G. Leidenfrost, De aquae communis nonnullis qualitatibus tractatus, (A tract about some qualities of common water) Ovenius, Duisburg, 1756; translated at, C. Wares and K. J. Bell, On the fixation of water in diverse fire, International Journal of Heat and Mass Transfer, 9 (1966) 1153-1166. [Back]
b D. R. Stull, Vapor pressure of pure substances. Organic and inorganic compounds, Industrial & Engineering Chemistry, 39 (1947) 517-540. [Back]
c C. Antoine, Tensions des vapeurs; nouvelle relation entre les tensions et les températures" [Vapor Pressure: a new relationship between pressure and temperature], Comptes Rendus des Séances de l'Académie des Sciences (in French), 107 (1888) 681-684, 778-780, 836-837 [Back]
d Ideal gas. All molecules in an ideal gas move widely separated along paths unaffected by intermolecular forces, and all collisions are perfectly elastic. Ideal gases obey the Ideal gas law, PV = nRT where P, V, T, and n are the pressure, volume, temperature, and the amount of substance, and R is the ideal gas constant. For an ideal gas, the fugacity equals the pressure. The ideal gas law is a good approximation of the behavior of many gases under many conditions. Most gases behave like ideal gases at higher temperatures and lower pressures when intermolecular forces and molecular size become less important. [Back]
e The air we breathe out is water-saturated for gas in contact with bodily fluids, but as this is slightly salty. it contains less water than would be if it had been in contact with pure water. It is about 95% saturated and at 35 °C. If the outside air is at 50% saturation, the exhaled breath will not condense above 12 °C. [Back]
Home | Site Index | Water phase diagram | LSBU | Top
This page was established in 2017 and last updated by Martin Chaplin on 19 February, 2022