Water Phase Diagram

The properties of all the known phases of water are described.

Phase diagrams
The phase diagram of water

'Corresponding to the abnormal behavior of the liquid at low pressures, and probably connected to it, the solid also shows abnormal behavior...'

Percy Bridgman, 1911 [2472]

Phase diagrams

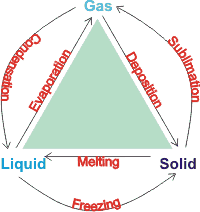
Phase diagrams show the preferred physical states of matter at different thermodynamic variables, such as temperatures and pressure. Within each phase, the material is uniform with respect to its chemical composition and physical state. At typical temperatures and pressures on Earth (marked by an 'E' below), water is a liquid, but it becomes solid (that is, ice) if its temperature is lowered below 0 °C and gaseous (that is, water vapor) if its temperature is raised above 100 °C, at the same pressure. Each line (phase line)^d on a phase diagram represents a phase boundary and gives the conditions when two phases may stably coexist in any relative proportions (having the same Gibbs free energy and identical chemical potential). Here, a slight change in temperature or pressure may cause the phases to abruptly change from one physical state to the other. Where three phase lines join, there is a 'triple point' when three phases stably coexist (having identical Gibbs free energies and identical chemical potentials),^d but may abruptly and change into each other given a slight change in temperature or pressure.

The Gibbs phase rule states that if a system consists of C components and P phases existing in equilibrium, the number of degrees of freedom (F, like temperature or pressure) is given by F = C − P + 2. Under the singular conditions of temperature and pressure where liquid water, gaseous water, and hexagonal ice stably coexist (P = 3), there is a 'triple point' (F = 0) where both the boiling point of water and the melting point of ice are equal for a single component system (C = 1), like pure water. Four phase lines cannot meet at a single point. A 'critical point' occurs at the end of a phase line where the properties of the two phases become indistinguishable from each other, for example when, under singular conditions of temperature and pressure, liquid water is hot enough, and gaseous water is under sufficient pressure that their densities are identical (0.322 g cm⁻³ ). At temperatures above the critical temperature, a gas cannot be liquefied. Critical points are usually found at the high-temperature end of the liquid-gas phase line.

The phase diagram of water

The phase diagram of water is complex,^a^,b^,c,e^,f [3921] having several triple points and one, or probably two, critical points. Many of the crystalline forms may remain metastable in much of the low-temperature phase space at lower pressures. An example of this is the metastable extension of the liquid phase line at low temperatures (< -21.985 °C ) through the ice III and ice II phase spaces, giving a metastable triple point (-32.7 °C and 273 MPa) that interlinks the three metastable equilibrium curves: ice Ih + ice IV, ice Ih + liquid and ice IV + liquid [3736]. A thermodynamic model of water and ices Ih, III, V, and VI [1320], and thermodynamic functions of the phase transitions [1658] have been described. The known ices can be divided, by cluster analysis of their structures [1717], into the low-pressure ices (hexagonal ice, cubic ice, and ice-eleven), the high-pressure ices (ice-seven, ice-eight, and ice-ten) and the others (found in the relatively narrow range of moderate pressures between about 200-2000 MPa). It is noticeable that most phase boundaries between the ices that share phase boundaries, particularly are parallel to the temperature axis, implying density-driven phase transformations [2465]; entropy-driven phase transformations, such as ice Ih-liquid water, show phase boundaries parallel to the pressure axis. All phases that share phase boundaries with liquid water (ices Ih, III, V, and VI and VII) have disordered hydrogen bonding. The phases with ordered hydrogen bonding are found at lower temperatures and are indicated in light blue below. The structural transformation conditions of some of these ices during compression have been described [1795]. As pressure increases, the ice phases become denser. They achieve this by initially bending bonds, forming tighter ring or helical networks, and finally including network interpenetration. This is particularly evident when comparing ice-five with the metastable ices (ice-four and ice-twelve) that may exist in its phase space. Note that, in the phase diagram below, only the stable phases are shown and that the vertical axis has a logarithmic scale for pressure, as the required pressures vary over more than ten orders of magnitude. Gibbs energy representations, densities, and phase lines for ice II, III, V, and VI have been reported [3832]. The SeaFreeze package allows the computation of the thermodynamic (phase boundaries, density, entropy, specific heat, isothermal bulk modulus, adiabatic bulk modulus, thermal expansivity, chemical potentials) and elastic properties of water and ice polymorphs (II, III, V, and VI) over the 0-2300 MPa and 220-500K range (covering the range of conditions encountered in hydrospheres in our solar system). The use of this package gives rise to some minor changes to some of the phase lines below. The phase diagram of water showing stable ice polymorphs relevant to water-rich planetary body interiors has been described [3832]

The phase diagram of water

Water phase diagram

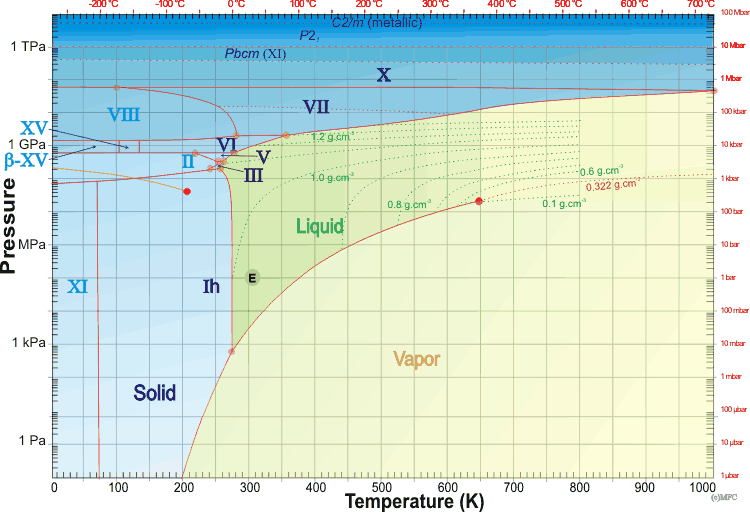
Detail of the water phase diagram

Mouse over the pressure border for D₂O phase lines

The mean surface conditions on Earth, (also atmospheric conditions, Mars and Venus on mousing over Earth) are indicated. The complex central part of the phase diagram is expanded opposite. The critical point and the orange line in the ice-one phase space refer to the low-density (LDA) and high-density (HDA) forms of amorphous water (ice) [16]. Although generally accepted and supported by diverse experimental evidence [754a, 861 ], the existence of this second, if metastable, critical point is impossible to prove absolutely at present and is disputed by some [200, 618 , 628 , 754b, 1115 ]. The transition between LDA and HDA is due to the increased entropy and attractive van der Waals contacts in HDA, compensating for the reduced strength of its hydrogen bonding.

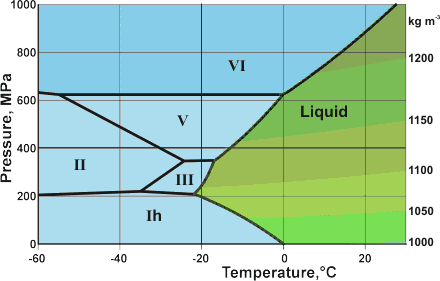
Positions of metastable and ordered ices , from [4290] — Positions of metastable and ordered ices, from [4290]

The high-pressure phase line between ice-ten (X) and ice-eleven (XI) [81] is still subject to experimental verification. The melting point line between supercritical water and high-pressure ice has been established [691 , 2096 ]. Ice VII possesses higher and lower pressure forms [1428 , 3509]. Phase diagrams of water at higher temperatures, up to 9000 K, have been proposed [1671 , 3199 ]. The area of stability of ice-eighteen (XVIII) is given elsewhere Both the critical points are shown as red circles in the phase diagram above.

Phase diagram of water at extreme P and T

from [4362] — Phase diagram of water at extreme pressure and temperature

from [4362]

A phase diagram of water at extreme pressures (up to 160GPa) and temperatures (up to 5000 K) is available, see right, ([4362] also compares prior work). The stability regions for the two superionic phases, face-centered cubic oxygen atoms, fcc-SI, and body-centered cubic oxygen atoms, bcc-SI, are indicated. The data was obtained using synchrotron X-ray diffraction and optical spectroscopy measurements of water in a laser-heated diamond anvil cell. The densities of

Many properties of cold liquid water change above about 200 MPa (for example, viscosity, self-diffusion, compressibility, Raman spectra, and molecular separation), which may be explained by the presence of a high-density liquid phase containing interpenetrating hydrogen bonds. The chemical properties of water are also greatly changed at high temperatures and pressures due to the changes in dissociation, solubility, diffusivity, and reactivity due to decreasing hydrogen-bonding [1116 ].

[Back to Top ]

Triple points

Triple points occur where three phase lines join, and the three (stable) phases may coexist at equilibrium. As the water triple point (gaseous water:liquid water:ihexagonal ice) can be precisely reproduced in the laboratory, its temperature (originally defined in 1954 to be precisely 273.16 K), together with the absolute zero of temperature (0 K) initially determined the thermodynamic temperature scale and the size of the kelvin (up until 2019). At the triple point of water, small heat inputs or outputs, or small attempts at compressions or expansion, will cause the relative amounts of gas, liquid, and ice Ih to vary without actually changing the equilibrium temperature or pressure of the system; such that the temperature and pressure stabilize on the highly precise, invariant and reproducible triple point value, so long as gas, liquid, and ice Ih remain present.

**Thermodynamic data for the triple points of water**
Triple points			MPa	°C	ΔH, kJ ˣ mol⁻¹	ΔS, J mol⁻¹ K⁻¹	ΔV cm³ mol⁻¹	Ref.	D₂O [717 ]
gas	liquid	Ih	0.000611657	0.010				536	661 Pa, 3.82 °C [70]
			gasliquid		-44.9	-165	-22050	1833
			gasIh		-50.9	-186	-22048
			liquidIh		-5.98	-22	1.634
gas	Ih	XI	0	-201.0				717	0 MPa, -197 °C
gas	Ih	XI	Ih XI				0
liquid	Ih	III	209.9	-21.985				537	220 MPa, -18.8 °C
			liquidIh		-4.23	-16.9	2.434	1833
			liquidIII		-3.83	-15.3	-0.839
			IhIII		0.39	1.6	-3.273
Ih	II	XI	89.6	-198.1				3832
Ih	II	XI	70	-199.8				2300	80 MPa, -195 °C [2300]
Ih	II	III	209.9	-34.15
			212.9	-34.7				537	225 MPa, -31.0 °C
			IhII		-0.75	-3.2	-3.919	1833
			IhIII		0.17	0.7	-3.532
			IIIII		0.92	3.8	0.387
II	III	V	355.5	-23.75				3832
			344.3	-24.3				537	347 MPa, -21.5 °C
			IIIII		1.27	5.1	0.261	1833
			IIV		1.20	4.8	-0.721
			IIIV		-0.07	-0.2	-0.982
II	VI	XV	828.5	-143.15				3832	≈ 0.8 GPa, -143 °C [1582 ]
liquid	III	V	350.1	-16.986				537	348 MPa, -14.5 °C
			liquidIII		-4.61	-18.0	-0.434	1833
			liquidV		-4.69	-18.3	-1.419
			IIIV		-0.07	-0.2	-0.985
II	V	VI	670.8	-71,25				3832
II	V	VI	≈ 620	≈ -55				539
liquid	V	VI	632.4	0.16				537	629 MPa, 2.4 °C
			liquidV		-5.27	-19.3	-0.949	1833
			liquidVI		-5.29	-19.4	-1.649
			VVI		-0.02	-0.5	-0.700
VI	VIII	XV						1582	≈ 1.5 GPa, -143 °C
VI	VII	VIII	2,100	≈ 5				8	1950 MPa, ≈ 0 °C
			VIVII		-0.09	-o.3	-1.0	1833
			VIVIII		-1.20	-4.2	-1.0
			VIIVIII		-1.10	-3.9	0.0
liquid	VI	VII	2,216	81.85				537	2060 MPa, 78 °C
			liquidVI		-6.36	-18.0	-0.59	1833
			liquidVII		-6.36	-18.0	-1.64
			VIVII		0.0	0.0	-1.05
VII	VIII	X	62,000	-173				538
super-critical fluid	VII	VII'	~20,000	~800				3509
super-critical fluid	VII	X	43,000	>700				612a
super-critical fluid	VII	X	47,000	≈ 727				612b
super-critical fluid	VII	XVIII	≈ 40,000	≈ 1000				1572

[Back to Top

]

Phase diagram of water, if it behaved like a more typical material of its molecular weight — Putative phase diagram of a 'typical' liquid

Footnotes

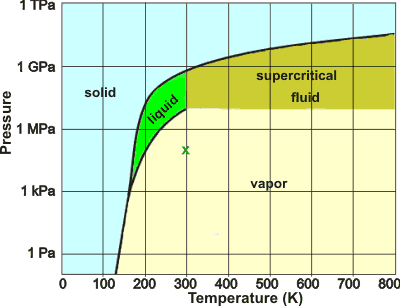
^a If water behaved more typically as a low relative molecular mass (molecular weight) material, its phase diagram might have looked somewhat like this (where 'x' marks ambient conditions on Earth). [Back]

^bThe metastable phases (Ice Ic, ice IV, Ice XII, and Ice XIII) do not belong in a phase diagram. However, Ice Ic (cubic ice) has been found in the hexagonal ice phase space below -80 °C, ice IV has been found within the ice-three, ice-five, and ice-six phase spaces, and Ice XII and Ice XIII have been found within the ice-two phase space. These phases may be stable for extended periods at low enough temperatures as there is insufficient energy available to overcome the necessary activation barriers. [Back]

^c Note that phase diagrams originating at this site have been copied by various sources, including to and then from Wikipedia without proper citation (or inherent permissions) of their source. Such poor scientific etiquette is easy for me to detect and reflects poorly on these authors. [ Back]

^d The Clausius Clapeyron equation. On a phase line, the Gibbs free energies of the two phases (G₁, G₂) must be equal and remain equal if conditions change, causing movement along the phase line. Thus

But, where S is the entropy, and where V is the volume

Therefore,

where L is the latent heat (enthalpy change) for the phase change. This is the Clausius-Clapeyron equation. It can also be stated as

dT/dP = TΔV/ΔH = ΔV/ΔS

where P, T, H, V, and S are the pressure, temperature, enthalpy, volume, and entropy. This may be extended to be

dT/dP=T(sign α₂V₂ - sign α₁V₁)ΔV/ΔH

where α represents the thermal expansion coefficients, for use with phases with negative expansion coefficients including the ice phase changes,

LDAIc, HDALDA, LDAHDA, IIIV, VVI, VIVII and VIVIII

[1147b]

When two or more phases are in equilibrium, the chemical potential of a substance is the same in each of the two phases and at all points in each of the phases.

μ_A = μ_B

Moving along a phase line

μ_A + dμ_A= μ_B + dμ_B

and

dμ_A= dμ_B

as dμ= -S_m dT + V_m dP (Gibbs equation) V_AdP − S_AdT = V_B dP − S_BdT

( V_A− V_B) ˣ dP = (S_A- S_B) ˣ dT

ΔV ˣ dP = ΔS ˣ dT

This gives the Clausius Clapeyron equation dP/dT = ΔS/ΔV = ΔH/TΔV

At a triple point, the Gibbs free energies of the three phases (G₁, G₂, G₃) must be equal and the entropy and enthalpy (latent heat) changes for all three phase changes (12, 23, 13) at that point may be calculated, given the pressure, temperature () and volume changes. [Back]

^eThe phase diagram for heavy water (D₂O) differs little from the diagram for H₂O given the scales used in the diagram. A more accurate representation would be by shifting the temperature scale by about 3.6 K as most of the triple points for D₂O are 3 - 4 K warmer than those for H₂O (see above). The pressure differences are positive or negative but not significant given the logarithmic scale used. [Back]

^fThe phase diagram of water for negative pressure has been described [2666 ]. [Back]