
Galileo Galilei,
the father of modern science
![]() Why do different methods give different water structures?
Why do different methods give different water structures?
![]() Dielectric spectroscopy
Dielectric spectroscopy
![]() Diffraction methods
Diffraction methods
![]() Modeling
Modeling
![]() Nuclear Magnetic Resonance (NMR)
Nuclear Magnetic Resonance (NMR)
![]() Osmotic stress
Osmotic stress
![]() Physical properties
Physical properties
![]() Vibrational spectra (Raman and infrared)
Vibrational spectra (Raman and infrared)
![]() Terahertz (THz) absorption spectroscopy
Terahertz (THz) absorption spectroscopy
![]() Microwave (GHz) absorption spectroscopy
Microwave (GHz) absorption spectroscopy
![]() Sum frequency generation
Sum frequency generation
![]() X-ray spectroscopy
X-ray spectroscopy
![]() Gaussian and Lorentzian curves
Gaussian and Lorentzian curves
![]() Raman versus infrared spectroscopy
Raman versus infrared spectroscopy
Water structuring is not easy to study
Several independent methods have been used to investigate the structure of liquid water and aqueous and biomolecular [2729] solutions. Although each method is often promoted as producing accurate results, the different methods produce conflicting conclusions. This not only generates academic disputes but also, and more importantly, causes general confusion and bewilderment leading to scientific disorientation.
Why do different methods give different water structures?
Each method produces data, but this data does not directly give the structure of water. It has to be interpreted. Any analysis depends on a theoretical base to interpret the data. More importantly, the results are only as good as this theoretical base, however excellent the quality of the data collected. In addition, different methods give information at particular time-, or size-scales and so may naturally differ.a Here is shown the principles behind the most important analytical methods (Dielectric spectroscopy, Diffraction, Models, Nuclear magnetic resonance, Physical properties, Vibrational spectra, X-Ray spectroscopy) and the main assumptions made to interpret their resulting data.
The structural forms and timescales for the different techniques are given below:
Structure |
Method(s) |
Time and size
scales |
|---|---|---|
Instantaneous |
X-ray absorption | ≈ 10−15 s, single molecule |
Almost instantaneous |
Infrared, Raman | ≈ 10−14- 10−13 s, single molecule - local cluster |
Vibrationally
averaged |
Models, Pump-probe laser | ≈ 10−12- 10−10 s, single molecule - local cluster |
Diffusionally
averaged |
Neutron scattering, NMR shift | ≈ 10−9-10−6 s, local cluster |
Probability |
X-ray diffraction, thermodynamics | > s, local cluster |
The structuring found depends on the timescale of the investigating methodology [2712]. Instantaneous structures show the actual positions and orientations of molecules, but these will be disordered relative to each other due to vibrational and linear and rotational diffusional motions; thus they will not show, or will show only poorly, any long-term or extensive order in the system. Slow processes, such as diffraction, show 'averaged' structures that may be a very poor representation of any structuring consisting of two rapidly interchanging structures. e Diffraction data shows long-term order but cannot determine whether the order is due to the same molecules being present in the same positions throughout or whether there are simply 'favored' positions with the molecules exchanging rapidly between them.
Attempts are being made to combine different techniques (X-ray absorption and emission, NMR shielding, and X-ray diffraction), with different time dependencies, to best fit various models [3716]. [Back to Top ![]() ]
]
Dielectric loss spectrum for ribonuclease
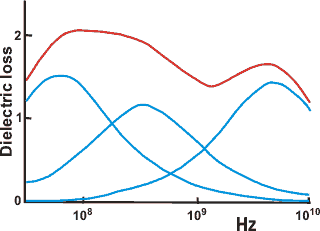
Dielectric spectroscopy [950, 3359] measures water tumbling and can detect water quantitatively
in different clusters if they are held by different average
hydrogen bond strengths. The dielectric loss is determined
over a wide frequency range (kHz-GHz). Slow tumbling (≈
ns) is due to tightly bound water, whereas fast tumbling
(≈ ps) is due to loosely bound water. Shown opposite is an example spectrum of a protein solution [785],
where the non-bulk water dielectric loss spectrum (red)
can be divided into three underlying Gaussian peaks. c Difficulty remains in unambiguously assigning the molecular
structures that produce these peaks. Dielectric spectroscopy does seem to show that long-range interactions (≈ 0.1 mm) are present in water [1630]. [Back to Top ![]() ]
]
Bragg's law for diffraction
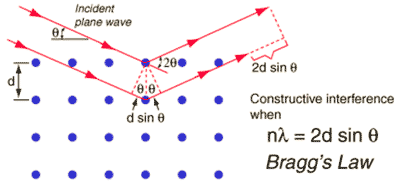
Diffraction methods make use of Bragg's law, involving the constructive interference of scattering (wavelength λ ≈ 1 Å, integer n) from regularly spaced atoms (shown as blue dots with spacing d, see right). Neutron diffraction determines nuclear atomic coordinates, whereas X-ray diffraction refers to the maxima of the electron density distribution. The timescale of X-ray and neutron scattering is very brief. Thus, diffraction methods [2553] involve the sum of a large number of instantaneous data from the many effectively frozen configurations of the sample. Thus, they measure the time-averaged distances between the atoms of water molecules. However, they cannot directly determine the cluster geometry. Also, the long-range hydrogen-bonded structure and correlations in liquid water cannot be determined by diffraction as there is no long-range positional order of molecules in a liquid, so any such conclusions drawn are meaningful only on the short scale (< ≈ nm).
Scattering from liquid water
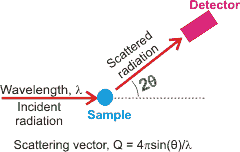
X-ray diffraction (~10 keV) is sensitive to the concentration of electrons (so not sensitive to isotopes). For ordered materials, such as the crystalline ices, the diffraction produces a series of regular spots related to the crystal symmetry. For disordered materials, like liquid water, the diffraction pattern consists of broad rings. It is first given in terms of the scattering vector (see left) and then translated into a derived radial distribution function. Even though there are twice as many hydrogen atoms as oxygen atoms in water, these electron-poor atoms contribute little (hydrogen atoms have ≈ 1/13 the electron density of the oxygen atoms and 2 ˣ 1/13 ≈ = 0.15), with ≈ 85% of the data being provided by the gOO(r) radial distribution function and the remainder from the gOH(r) radial distribution function [1024] (H - H interactions being less than 0.6 %). Methodology for detecting hydrogen atoms and X-H bonds has been developed, and this may be of great use in the future so long as the temperature is below 140 K and that the resolution is at least 0.6 Å [2604].
Radial distributions in ice Ih by neutron diffraction [154]
![Neutron diffraction of hexagonal ice at 220 K, from [154] Neutron diffraction of hexagonal ice at 220 K, from [154]](images/iceneu.gif)
Neutron diffraction utilizes the wave property of slow neutrons produced in an atomic reactor (≈ 0.1 eV, ≡ ≈ 1 Å). It is sensitive to nuclei (including isotopes) and can determine the positions of light atoms, such as hydrogen. The strength of the interaction between the neutron and a nucleus is called the scattering length, which is specific to each isotopic nucleus (b, in femtometers, fm). Interference terms in the scattering from pairs of atoms give rise to coherent scattering, whereas scattering from all individual atoms gives rise to incoherent scattering. For water, neutron diffraction needs mixtures of D2O, HDO, and H2O as H atoms are strong incoherent scatterers, whereby the scatter contains no structural information. Such mixtures produce data with less precision and accuracy as such mixtures structure water differently from pure H2O.
Selected neutron scattering lengths and cross sections g
Isotopic nucleus |
bcoherent
, fm |
bincoherent , fm |
cross sectioncoherent , b |
cross sectionincoherent , b |
1H |
-3.7406 |
25.274 |
1.7583 |
80.27 |
2H |
6.671 |
4.04 |
2.05 |
7.64 |
12C |
6.6511 |
0 |
5.559 |
0 |
13C |
6.19
|
-0.52 |
4.81 |
0.034 |
14N |
9.37 |
2.0 |
11.03 |
0.5 |
16O |
5.803 |
0 |
4.232 |
0 |
31P |
5.13 |
0.2 |
3.307 |
0.005 |
32S |
2.804 |
0 |
0.9880 |
0 |
First radial distances
Neutron diffraction gives gOO(r), gOD(r), and gDD(r) radial distribution data, which does allow some, if incomplete, orientation information to be extracted for neighboring water molecules. The results generally need much interpretation and help from modeling [2405]. Thus even crystalline ice Ih gives rise to artifactual peaks, see the O···O peaks at 2.43 Å and 3.45 Å opposite. Also, the widths of the peaks are greater than might be expected for a crystalline structure. The major drawback of neutron diffraction is the cost of the nuclear reactor facility with its intrinsic risk and poor accessibility for research.
Electron diffraction can only be used on thin films (~1 µm even at MeV energies) due to its strong scattering [4150]. Wide-angle X-ray diffraction has confirmed the existence of two distinctly different hydrogen-bonded environments in liquid water [1755]. The (coarse) radial distribution function of liquid water using electron scattering has been achieved [4200].
The use of diffraction methods for studying the hydration structure of alkali ions has been reviewed [1062]. Diffraction data may be refined by fitting water model simulations [1245]. The resulting fit, however, is insensitive to the model chosen [888], such that optimizing the model to the fit does not, perforce, produce a better model. Diffraction results are discussed further elsewhere. Diffraction methods give data little different from bulk water beyond the first hydration shell, where other methods indicate changed structure [1427].
Diffraction methods are excellent for testing models of water structure but less helpful for delivering the fundamental structure of water due to the difficulty in obtaining orientation information and correlations at intermediate distances. However, as the instrumentation has improved, the local dynamics of water in real space and time, such as viscosity and diffusion, have been visualized by inelastic X-ray and neutron scattering measurements. It makes use of the Van Hove function (VHF)
![]()
where ri(t) is the position of the atom i at time t, i = 1, 2, . . . N, and ρ0 is the atomic number density of the system [3741]. [Back to Top ![]() ]
]
Many molecular models for water are described on another
page of this site. An underlying assumption of these
models is that the structure of liquid water may be modeled
using just two-body effects (that is, molecule A affects
molecule B independently of molecule C affecting molecule
B) and do not include any contribution from any covalency in their interaction. Models for liquid water have, so far,
proved to be poor predictors for physical and molecular
properties outside those used in their development and parameterization.
Modeling studies may result in a picture of an 'average'
liquid water molecule, which may be misleading as such 'average'
structures do not exist in most ice phases and may not be
relevant to liquid water. [Back to Top ![]() ]
]
Water contains three isotopes of use in NMR. d
NMR, H2O atoms |
1H |
2H |
17O |
|---|---|---|---|
Spin states |
+½, -½ |
1, 0, -1 |
5/2, 3/2, 1/2, -1/2, -3/2, -5/2 |
Relative natural abundance (%) |
99.985 |
0.015 |
0.048 |
Relative sensitivity at natural abundance |
1 |
1.4 ˣ 10−6 |
1.1 ˣ 10−5 |
26.7522 ˣ 107 |
4.1066 ˣ 107 |
-3.6281 ˣ 107 |
|
Frequency at 2.3488 T (MHz) * |
100 |
15.3506 |
13.5565 |
* data from WebElements.
The 1H and 2H NMR spectra can be used to quantify the deuterium atom content of H2O, HDO, D2O mixtures from the natural abundance to nearly 100% [1817]. As it has been reported that magnetic fields may alter the clustering of water ([192, 485, 647]), then the results of NMR must be considered with this possibility in mind. Another possible weakness of using NMR is that only ortho-water is NMR-active, para-water having no intrinsic magnetic moment [835]. However, all unpaired protons are NMR-active (not just ortho-water), and the exchange of protons may be rapid compared with gathering the NMR signal [2118].
NMR analysis generally gives reduced information due to proton exchange and movement of water between environments. The average proton residence time on a water molecule is about a millisecond at 25 °C and pH 7, being less than that at other pHs or higher temperatures. Therefore, only single, population-weighted averaged 1H, 2H, or 17O NMR peaks are generally seen in aqueous solutions. The exception to this is where separate non-exchanging or very slowly exchanging pools of water molecules are found.
Water's NMR chemical shifts (17O and 1H) are affected by ions in solution with increasing ionic radius generally causing an increased deshielding effect on the water oxygen atoms but a decreased deshielding effect on the water's protons [781]. The effects are linearly concentration-dependent with a change in the slope found above the concentration that causes a minimum in the specific heat (≈ 2-3 M) [556]. Here, the charge density effect (greater charge density causing greater deshielding), as seen in the division of ions into kosmotropes and chaotropes, is less important than the ionic size effect [781]. As larger ionic size results in an increased number of first shell water molecules interacting with the ion's field within the clathrate surroundings, the apparent shielding change may be due to an increased effect on the average shift.
NMR spectroscopy is one of the most valuable methods for experimentally characterizing H-bond interactions in biological systems [3347] and often provides the strongest evidence for any partial covalent character. The 1H-shielding values of the H-bond proton are determined by the depletion of electronic density around the bonding hydrogen atom, which stems from the H-bond formation. Both 1H and 17O NMR peaks shift to downfield (greater ppm) with increasing hydrogen bond strength; in the case of 17O, the donor O shift increasies more than the acceptor O reduces. However, only ‘averaged’ water environments may be obtained. Where several aqueous environments exist, the 1H NMR spectrum (mainly just one broad peak) may be deconvoluted into Gaussian sub-bands due to differing degrees of hydrogen-bonded water with greater chemical shift (that is, ppm), indicating stronger hydrogen bonding and greater tetrahedrality of the water clustering [851].
The changes in the motion of interfacial water molecules on thawing their ices, detected using NMR, can characterize the dynamic structure of proteins so adding considerably to the information available from protein 3-D structural determination [2249]. NMR has been used to estimate changes in water's hydrogen bond lengths and strengths [458]. Such investigation makes use ab initio calculations to interpret changes in the longitudinal relaxation τ1 (see below) of HDO in D2O solution by assuming (somewhat incorrectly) that this mixture has a similar structure to pure H2O.
The NMR signal undergoes two relaxation processes; spin-lattice (longitudinal) relaxation resulting in the decay of the spin distribution (τ1) and spin-spin (transverse) relaxation (τ2) resulting in the loss of the spin coherence. τ2 is inversely proportional to the width (at half height) of the NMR peak. τ1 is 3.6 s at 25 °C due mostly to dipole-dipole couplings [430]. As τ1 reduces with increasing dissolved molecular oxygen concentration (due to its paramagnetic nature) [782] and dissolved oxygen concentrations are expected to be greater in more hydrophobic environments near hydrophobic surfaces, dissolved oxygen is capable of giving rise to artifacts in the NMR spectra of water. Such effects may change over a period of several days [294].
Variation of NMR relaxation times, from [581]
![Variation of NMR relaxation times with order in liquid water; from [581] Variation of NMR relaxation times with order in liquid water; from [581]](images/nmr_relaxation.gif)
Shorter τ2 values indicate less molecular mobility. The 1H τ2 of water at 25 °C, viscous water and ice at 0 °C are about 3 s, ≈ 1 ms, and ≈ 5 μs respectively. However, the T2 relaxation times are also reduced by exchange reactions with, for example, proteins carboxyl, hydroxyl, and amine groups. Generally only single, population-weighted averaged, 1H, 2H or 17O relaxation rates are seen in aqueous solutions. The exception to this is where separate non- (or very slowly) exchanging pools of water molecules exist such as occur in porous media including biological tissue and many foodstuffs. τ1 and τ2 are approximately equal for liquid water, both dropping with increased hydrogen-bonded clustering (for example, increased viscosity) under normal conditions. However, as the degree of tetrahedral clustering increases further, τ1 increases asτ2 decreases [581]. τ1 thus shows a minimum at intermediate viscosity (rotational correlation time), f at the NMR resonant frequency, whereas τ2 decreases continuously with increasing viscosity. Note that NMR relaxation is a non-equilibrium kinetic event and cannot give thermodynamic quantities such as water activity.
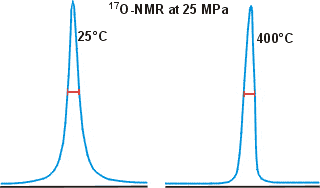
17O has been used to estimate water clustering using NMR line-width measurements where strongly clustered water gives broader peaks. However, this reasoning is faulty, and the data is often imprecise and probably affected by dissolved O2 and pH; see also, Paul Shin's critique of this method.
Shown opposite are the 17O NMR peaks for water at widely different temperatures, showing how little the width changes even under such different conditions [783].
Nuclear Overhauser effects (NOEs) may be used to identify relatively static water molecules within the first hydration shell (<≈ 0.5 nm) around biological molecules [784].
Apparent diffusion rates of water are measured using magnetic
field gradients [652,2112] and may be incorporated into magnetic resonance
images (MRI). As diffusion is restricted in more extensive
aqueous clusters, this method can differentiate different
pools of water by their mean diffusion rates. NMR relaxation measurements can give the rotational diffusion coefficients using the natural 17O abundance [652, 2112]. [Back to Top ![]() ]
]
Osmotic stress [2006, 2113] is complementary to other physical techniques in that it probes the changes in hydration that accompany biologically relevant processes from their dependence on osmotic pressure (water activity). For example, the number of thermodynamically unique water molecules associated with the double helix and released from the single strands upon melting may be determined from the depression of melting temperature upon decreasing the water activity [2113]. [Back to Top ![]() ]
]
Physical properties such as viscosity, compressibility, the speed
of sound, heat capacity, refractive index, thermal
conductivity, and surface tension can all be used to gather information concerning the structure
of water. The interpretation of this data is not clear-cut,
however. Note that only the surface properties, not the
bulk properties, are discovered using surface tension. The
surface structure of water is very different from the bulk
structure and may mislead. [Back to Top ![]() ]
]
Water's OH stretch peak, divided into gaussian peaks
![Water's OH stretch peak, divided into two gaussian peaks, from [4411] Water's OH stretch peak, divided into two gaussian peaks, from [4411]](images/busing.gif)
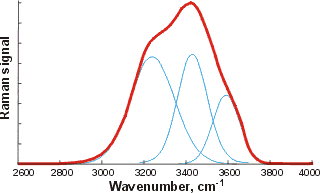
![The OH stretch peak of water at about 3400 cm-1, divided into four underlying gaussian peaks, from [1980] The OH stretch peak of water at about 3400 cm-1, divided into four underlying gaussian peaks, from [1980]](images/ramanpk3.gif)
![The OH stretch peak of water at about 3400 cm-1, divided into five underlying gaussian peaks, from [4408] The OH stretch peak of water at about 3400 cm-1, divided into five underlying gaussian peaks, from [4408]](images/ramanpk.gif)
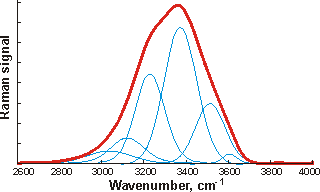
The curve fittings attempt to optimize the overlapping band profile starting from a predetermined set of individual bands and the estimated baseline [4416]. As each band (Gaussian peak) uses three optimized parameters (position, height, and width at half height), the number used varies between six and eighteen. The more parameters fitted to an experimental curve, the better the fit. However, this number of fitting parameters should be minimized. Using even more sub-bands would inevitably lead to better fits (despite what is concluded in [1318]) but at a high cost in fitted parameters. This is particularly true as the Gaussian peaks (if used) have differing widths (as seen above) because they contain different numbers of underlying structures. The envelopes can give rise to different well-fitted sub-peaks but with the same number of peaks. The appropriateness of the final fit is down to the experience and judgment of the researcher with little input from the computer, as similar results may be obtained from different computer analyses. The fitted parameters for the Gaussian peaks, assignations, and residuals vary between researchers and between works by the same author. The choice of initial parameters influences the final result. Allowing for minimizing the number of required fitted parameters, perhaps the most acceptable fits are produced by just three sub-peaks. The final peaks may not necessarily be symmetrical as a continuum of many individual bands contributes to them. The envelope has an isosbestic point on increasing the temperature, between the two prominent peaks where the 3200 cm−1 peak goes down as the 3400 cm−1 peak goes up.
Water gives complex infrared and Raman spectra [1738, 2627],h and seriously affects the spectroscopy of aqueous solutions [ 4071]. Analysis of these, together with changes caused by variations in temperature or pressure, the presence of solutes, or the presence of D2O, is thought to provide detailed information concerning liquid water structuring. Liquid water spectra reportedly correspond to linear mixtures of just two contributing forms [1738].b Due to peak broadening caused by the varying interactions between neighboring molecules, the spectra may be analyzed by supposing several Gaussian-shapedc vibrational absorptions underlying the complex peaks. Difficulties in the analysis concern determining how many absorption peaks are present and the molecular origins of these vibrations. The more vibrations that are thought to contribute to a complex absorption peak, and thus the more parameters involved, the better may be any produced fit.
For many years Raman spectroscopy of liquid water has been used to understand the structuring of the hydrogen bonding in liquid water. In particular, the 3400 cm−1 Raman peak envelope has been analyzed using several Gaussian or Lorentzian curves,c see right. The envelopes are preferentially fitted to underlying peaks and then smoothed. In general, the more parameters fitted to the experimental curve, the better the fit. It is not surprising that the more fitted curves, the smaller the residuals. There are very many questions to be asked within this argument. What shape should the underlying peaks be? How many structures are associated with the individual peaks? How certain can the structures associated with the peaks be described? Should the residuals or the number of fitting parameters be minimized? Are these peaks quantitatively associated with the number of included vibrating structures? If so, should the peak height or area be the quantitative factor? Can analysis of the spectra drive the understanding of the structuring in liquid water or vice versa?
Raman spectroscopy has been closely tied to discovering the structure of water. The 3400 cm-1 Raman peak envelope appears to give helpful information concerning the structure of liquid water. But does it? The derived information depends on the theory used, and circular arguments support themselves. Many researchers over almost 100 years have tackled this task. Their papers develop wide-ranging and confusingly different analyses.
However, water structuring is now firmly established from other methodologies as best interpreted using a two-state water mixture [2653]. This idea may help the Raman analysis, but other factors must be considered. The assignment of symmetric stretch, asymmetric stretch, and bending overtone is usually discarded in favor of the assumption that combined O-H stretch vibrations are shifted due to local hydrogen-bonding arrangements. However, and importantly, there is no consensus about the number of underlying absorption peaks with different researchers using two, three, four, five, or six absorptions, as shown indicatively opposite.
The vibrations associated with the O-H groups depend on any attached hydrogen bonding strength. Strong hydrogen bonding is associated with lower frequencies (smaller wavenumbers), and weaker hydrogen bonding is associated with higher frequencies (greater wavenumbers). If the O-H hydrogen atom is free, without any hydrogen bonding, then the frequencies of the vibrations are at their highest with a higher wavenumber (~3600 cm−1). As the relative strength of hydrogen bonding is determinable by modeling, the ordering of the peaks across the envelope might be expected to be clear-cut from the most strongly hydrogen-bonded, through the slightly hydrogen-bonded, to the non-hydrogen-bonded.
Initially, the peaks forming the 3400 cm-1 envelope were thought due to the symmetric stretch and asymmetric stretch vibrations and the first overtone of the bend vibration. Over time it has been realized that the individual stretch vibrations of each O-H bond contributed separately but additively, and the bend overtones have lesser importance. This is because few O-H bonds are energetically symmetrical about their oxygen atoms. All probably have some hydrogen bond character. This fact has become apparent from the mixed vibrations found in H2O, HOD, and D2O mixtures, where no significant vibrations have been found separately from the combinations of the vibrations from the HOD molecules. Further confusion of the Raman spectroscopy is that the Raman excitation wavelength affects the peaks in the 3000-3700 cm-1 range [1536]. In particular, the component at about 3200 cm-1 is in resonance with visible red light from a vibrational overtone.
The two most significant peaks at about 3200 cm-1 and 3400 cm-1 are most likely due to the expected greatest DDAA-OH (H2O with four hydrogen bonds, two donor and two acceptor at about 3200 cm-1) and DA-OH (H20 with two hydrogen bonds, one donor and one acceptor at about 3400 cm-1) vibrations, respectively, containing many second-neighbor variations. These sub-peaks change their relative sizes (the DDAA-OH peak decreasing and the DA-OH peak increasing) with increasing temperatures [4408, 4417]. Both peaks reduce and then disappear at high temperatures. Although the 3200 cm-1 peak was initially assigned to the second overtone of the bending peak [4413], this peak is now generally accepted as a stretch peak. These peaks probably include lesser peaks within their areas. Assigning these significant peaks to the expected greatest DDAA-OH and DA-OH vibrations agrees with the two-state structuring hypothesis for liquid water that has gained wide acceptance [2653]. The peaks, however, are not due to single vibrations but to a multitude of related vibrations due to different hydrogen bonding strengths. It remains to hypothesize what shapes these combined peaks should have. Often Gaussian or Lorentzian peaks are used for convenience,c but there is no solid underlying theory for such a mixture of vibrations. Both Gaussian and Lorentzian curves fit well into the envelope, taking up three fitting parameters. As the 3400 cm-1 envelope has a broadened base, the Lorentzian peaks fit somewhat better at the extremes without fitting any less well with the upper parts of the peaks. The residuals of the most prominent peaks contribute the most to the 'fit' rather than those at the extrema and perhaps should be scaled in any comparisons. However, the choice for the mathematical formula used is personal rather than scientific.
The hydrogen-bond strengths of the two hydrogen bonds associated with the stretch vibrations of H2O depend on positioning the first four neighbors to the central water molecule and its twelve outer neighbors. The positioning of these neighbors gives between about nine (at different energies or different primary structures [4412]) and 400 (with different structures including the first and secondary hydrations) optimum structures with continua of in-between values being allowed [852]. A helpful way of describing the cooperative/anti-cooperative nature of the water dimer hydrogen bond is to use the nomenclature d'a'DAd''a'' where DA represents the donor-acceptor nature of the hydrogen bond in question, the d'a' represents the remaining donor-acceptor status of the donating water molecule and d''a'' represents the remaining donor-acceptor status of the accepting water molecule (for examples see elsewhere) [852]. Individually, the most energetically favored donating water molecules have the structures 02DAxx, 12DAxx, 01DAxx, and 11DAxx, with 00DAxx and 10DAxx disfavored. The most energetically favored accepting water molecules have structures xxDA20, xxDA21, xxDA10, and xxDA11, with xxDA00 and xxDA01 disfavored.
The Raman O-H stretch envelope around 3400 cm-1 is often broken down into a few symmetrical Gaussian peaks that were thought to correspond to hydrogen-bonded water molecules with different donor (D) and acceptor (A) hydrogen bonds. The possession of a donor hydrogen bond O-H···OH2, (shown by the dots) reduces the vibrational frequency. This hydrogen bond is strengthened by the oxygen atom accepting hydrogen bonds from neighboring water molecules. Assignations of the lesser surrounding peaks at about 3000 cm-1 and 3600 cm-1 are less clear. The DAA-OH peak as assigned at about 3000 cm-1 seems out of place at first compared with the DDAA-OH peak; why is it at a shorter wavenumber, rather than lying between the DDAA-OH and DA-OH peaks. It was initially assigned based on calculated spectra [4409]. Indeed, the hydrogen bond associated with the DAA-OH is marginally stronger than either of the hydrogen bonds associated with DDAA-OH. This DAA-OH vibration is a single stretch and does not involve the free O-H left on the H2O molecule, probably associated with the 3600 cm-1 peak. However, this small 3000 cm-1 band may be an overtone bend vibration and not belong to those associated with the stretch vibrations, with the small DAA-OH peak lying under the DDAA-OH peak. The band or bands close to 3600 cm-1 are also likely mistakenly ascribed. Assignment of any peak to the free H2O is not probable as there is little support elsewhere for the presence of totally free H2O molecules in liquid water at ambient temperatures. However, singly-linked H2O molecules may be present if held by their acceptor hydrogen bond(s).
There are no free water molecules present, but the peak at the greatest wavenumber may be due to the combination of A-OH and AA-OH peaks. It is expected that the DDA-OH peak should lie at a lower wavenumber than the DA-OH peak. It is not likely to be very different, however, and may be hidden under the DA-OH peak. Any free O-H associated with the DAA-OH, DDA-OH, DA-OH, A-OH, and AA-OH groups should all be at about the 3600 cm-1 end of the envelope. The expectedly prominent peak is not found here, rather upsetting this hypothesis and concluding that these peaks may be hidden under the DA-OH peak. Thus the two prominent peaks at about 3200 cm-1 and 3400 cm-1 may be mostly due to the hydrogen-bonded and non-hydrogen-bonded O-H peaks. However, as neither the peak heights nor the more precise peak areas are proven to correspond to the amounts of material present, it is difficult to derive much directly from the peaks fitted to the envelope.
These temperature variations may be linked to the more-recently discovered two-state liquid water. There are many more structural possibilities that should also be included, if they are present. The spectra must be associated with water's dipole moment (through their polarization), and the induced dipole moments are generated by their interaction with all the surrounding water molecules. The calculated dipole moments of water molecules with their immediate neighbors are shown below [3597]. The actual dipole moments depend on the total of all surrounding water molecules, but this indicates the increase in dipole moment with the increase in hydrogen bonding. On this basis, there should be between seven and nine sub-peaks. The accessible and singly-linked H2O would give Raman signals with the greatest wavenumbers and the completely hydrogen-bonded DDAA-OH structure at the lowest wavenumber.
Calculated dipole moments of water molecules with their immediate neighbors [3597]

At 295 K and 0.1 MPa, the Raman spectra of H2O and D2O have often been deconvoluted into five sub-bands (see the Raman spectra above left, from [2830]. Note that the outline curves have been considerably smoothed. Substantial residuals vary with the wavenumber and give many peaks and troughs on smoothing [4408]. Such analysis requires many (fifteen) fitted parameters. [1925] In this case, the five sub-bands are located at 3043 cm−1, 3225 cm−1, 3432 cm−1, 3575 cm−1, and 3638 cm−1 (H2O), or 2265 cm−1, 2382 cm−1, 2503 cm−1, 2590 cm−1, and 2666 cm−1 (D2O), which the authors assign to O-H (O-D) vibrations engaged in DAA-OH, DDAA-OH, DA-OH, and DDA-OH hydrogen-bonding, and free vibrations [1980, 2894]. The fitted parameters for the Gaussian peaks, assignations, and residuals vary between researchers and between works by the same author. They should not be thought of as exact. The two most significant vibrations are assigned to the doubly donor-acceptor (DDA-OH) or singly donor-acceptor (DA-OH) water molecules. Other workers assign different Gaussian peaks to this group, using different positions, and ascribe them to different causative structures [2972].
Peak a |
Water's assigned
hydrogen bond molecular linkages |
|||
|---|---|---|---|---|
0 |
unlinked | 1 bifurcated b, 1 trifurcated c | 2 H-bond, donors broken | 3636 cm−1, unlinked |
1 |
1 H-bond | 2 bifurcated | 2 H-bond, acceptors broken | 3572 cm−1, 3 H-bond, acceptor broken |
2 |
2 H-bond | 1 O-H H-bonded, 1 bifurcated | 3 H-bond, donor broken | 3430 cm−1,2 H-bond, acceptor and donor broken |
3 |
3 H-bond | Both O-H are weakly H-bonded | 3 H-bond, acceptor broken | 3220 cm−1, 4 H-bond |
4 |
4 H-bond | Both O-H are strongly H-bonded | 4 H-bond | 3014 cm−1, 3 H-bond, donor broken |
Ref. |
[786] |
[573] |
[699b] |
[1925] |
a From high to low wavenumber;
0 = greatest wavenumber.
b The O-H hydrogen bond is shared between two accepting
water molecules.
c The
O-H hydrogen bond is shared between three accepting
water molecules.
More confusion in the analysis is due to the lack of a consensus view as to what these underlying absorption peaks represent. It is unclear whether the numbers of hydrogen bonds are important [786], or is it the type of hydrogen bond (single, bifurcated, or trifurcated) [573], the hydrogen bond bending angles [439], the nature of the formed or broken donor and acceptor hydrogen bonds [699b], or the length of the hydrogen bonds [1318].Each of these has been argued (for example, see below), but the contributing vibrational peaks must contain all of these (and other) contributions. The absorption bands also reflect coherent vibrational transfer involving several to many water molecules [2003]. It is now believed that analysis involving individual water molecules and Gaussian peaks may be inherently flawed.
As we still do not fully understand the complex vibrations present in liquid water, setting up a model to understand the constituent contributions to the vibrational envelope is nigh impossible. This is why most analyses start with the spectrum and try to fit the most reasonable structures to the number of the sub-peaks present. Both Lorentzian and Gaussian curves [4414] are derived from the broadening of single vibrations due to environmental interactions. Neither are meant to represent large numbers of contributing peaks with different peak positions and widths. Gaussian curves are the best at representing this continuum of sub-peaks. As found, Lorentzian peaks can best represent peaks with extended bases but may give overall more significant residuals. A combination of the Gaussian and Lorentzian peaks in Voigt profiles does not improve the situation.
It should be recognized that the best mathematical (least squares) fit might not be the best fit for the underlying structures. Also, there will probably be several fits that ly close to the best fit, where the natural noise in the data allows for no clear-cut favorite. Any good fit has small residuals, but even then, various fits may have acceptably small residuals, with the operator's choice between them being down to their personal choice.
Two-dimensional Raman spectroscopy has been shown to provide information concerning water's intermolecular dynamics and may eventually provide data on the hydrogen bond network rearrangements responsible for water's anomalies [1097].
A thorough and careful analysis of the combination band centered at about 5260 cm-1 failed to distinguish the substructures that correlate with the vibrational sub-bands [909].
Using a pump-probe laser with 70-fs pulses at 3350 cm-1 (O-H stretch) and detecting the resultant molecular vibrations within the hydrogen-bonded clusters over a range of frequencies with time shows efficient energy redistribution [750]. However, this method is not yet able to show structuring details. Stimulated Raman excited fluorescence (SREF) microscopy using an IR fiber laser at 1031.2 nm has been developed into a water-sensing tool by coupling it with vibrational solvatochromism using Rhodamine 800. This technique has allowed the direct visualization of the spatially-resolved distribution of water states inside single mammalian cells [3787].
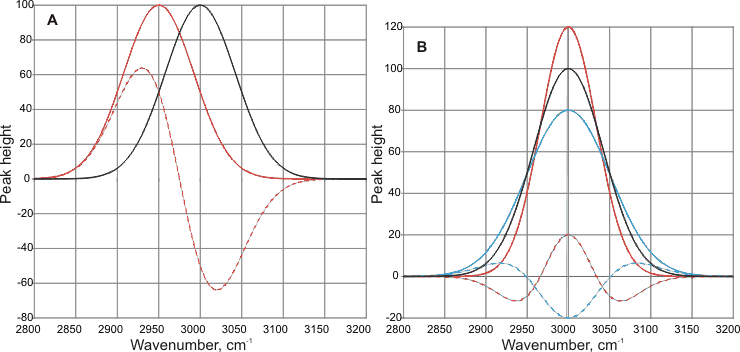
Care must be taken if the spectra of solutions are obtained by subtracting baseline Gaussian-like curves. This may give rise to peaks and troughs in unexpected non-physical positions (see below). In (A), the base peak (solid black line, given at 3000 cm-1 is shifted by the new conditions (solid red line) by -50 cm-1. The result of the subtraction of these peaks (dashed red line) gives a new peak (at -70 cm-1) in a position different from the peak, and a trough at +20 cm-1 with no apparent physical cause. In (B), the base peak (solid black line, given at 3000 cm-1 is broadened (solid blue line) or narrowed (solid red line) by the new conditions. The results of subtraction of these peaks (dashed lines) give new peaks and troughs with no apparent physical cause. The position of the peak has not shifted, but its subtracted curve may give a peak or a trough in this position plus neighboring peaks or troughs (see below).
The results of subtracting Gaussian curves.
Teraherz transmission by 100 mm liquid water, 4 °C
from [4469]
![Teraherz transmission by liquid water, 4 °C, from [4469] Teraherz transmission by liquid water, 4 °C, from [4469]](images/terahz.gif)
Terahertz fields oscillate on a picosecond timescale and so are inherently suited to study water where the dynamic network of hydrogen bonds rearrange at about the same timescale. Terahertz (THz) spectroscopy, two-dimensional Raman-THz spectroscopy [2050] (0.3 - 20 THz = 10 - 600 cm-1), and THz-FTIR spectroscopy may be used to investigate hydrogen bond network resonances, hydration dynamics, and water dynamics on the picosecond timescale [4352]. While NMR, and X-ray techniques are inadequate for describing the dynamics of the hydration layer (2 nm - 4 nm) surrounding biomolecules, THz spectroscopy has shown itself to be a powerful technique for this purpose [4286]. THz absorption spectroscopy probes the reorientation of permanent and induced dipole moments of clusters and, from the time-dependence of these fluctuations, it is able to determine the frequency and strength of the cluster motions [1783], and the effect of a solute on the collective motions of the hydrogen-bonded network. In particular, the librational resonances of liquid water that reflect water's hydrogen bonding, can be studied. Such spectroscopy can also be used to investigate the hydration layers around biomolecules [1196, 1427] and how they change during biological processes [2237]. This spectroscopy is powerful for examining changes in water mobility and shows changes in the water structuring at greater distances from biomolecules than those found using NMR or diffraction methods [1368, 1811]. The hydration state of solutions may be examined using terahertz time-domain attenuated total reflection spectroscopy, which makes use of the complete complex dielectric function; both the dielectric loss, due to relaxation motion of water, and the changes in the real part of the relative permittivity (dielectric constant) [1437].
Pump–probe experiments at 12.3 THz on liquid water, excite the librational mode [4488]. Comparison of the results obtained on a static sample and a free-flowing water jet, distinct contributions by thermal, acoustic, and nonlinear optical effects ere disentangled
[Back to Top ![]() ]
]
Rotational spectroscopy can be used in the gas phase for small water clusters. For example, broadband rotational spectroscopy has unambiguously identified the cage, prism, and book isomers of the water hexamer (H2O)6 [2260].
Sum frequency generation
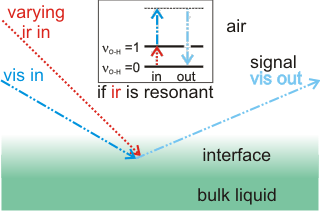
Sum frequency generation (SFG) and second harmonic generation (SHG) surface spectra are spectroscopic methods for investigating the surface of water without interference from the bulk liquid [2627, 3980]. The output spectra derive from a summed combination of input beams when the infrared frequency is in resonance with a vibration within the interface (for example, the O-H vibration of water, see right). As both the bulk aqueous solution and the gas phase are isotropic, they are not active in this spectroscopy, leaving just the anisotropic interfacial layer to provide the spectra due to a net orientation of surface molecular dipoles.
SFG spectrum of the water-vapor interface
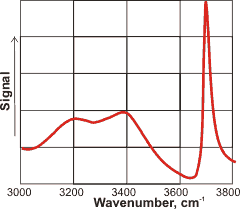
The depth of this anisotropy governs the depth probed but is not independently determined. It may extend out to the limit of the wavelength or Nernst layer although mostly affected within nanometers of the interface with a definite bias towards the very outside of an aqueous interface (containing a lower density of water molecules) rather than towards the bulk. As the spectra are acquired over periods of seconds, it is of interest that the surface mono-layer may be exchanged millions of times during this period [2408]. The result is that any spectral features are formed from a complex combination of spectra from within this ever-changing environment. For uncharged surfaces, the surface is only a molecule or two thick. However, when the surface is charged as is the case with water, the implied surface-specificity of this methodology is not warranted [4392]. The surface has the largest effect as can be seen from the SFG spectrum of the water-vapor interface shown left, where the surface-dangling OH groups give the most prominent peak at 3700 cm−1. As well as not determining the depth of the surface, a further limitation of the method is that it cannot give how the orientation of the molecules varies with distance from the surface. Simulations can help to uncover these factors [3946].
A version of this second harmonic generation methodology uses soft x-rays (between 100 eV and 1 keV) [3305]. This gives high interfacial specificity of the first few molecular layers of an exposed bulk sample or either side of a buried interface.
 X-ray-based techniques can be used to study the hydrogen-bond network of liquid water [1965, 2623, 4051, 4483]. As the techniques have attosecond timescales, they reflect the instantaneous molecular configuration of the water molecules. Difficulties interpretating these techniques are due to the lack of a robust theoretical understanding [2623].
X-ray-based techniques can be used to study the hydrogen-bond network of liquid water [1965, 2623, 4051, 4483]. As the techniques have attosecond timescales, they reflect the instantaneous molecular configuration of the water molecules. Difficulties interpretating these techniques are due to the lack of a robust theoretical understanding [2623].
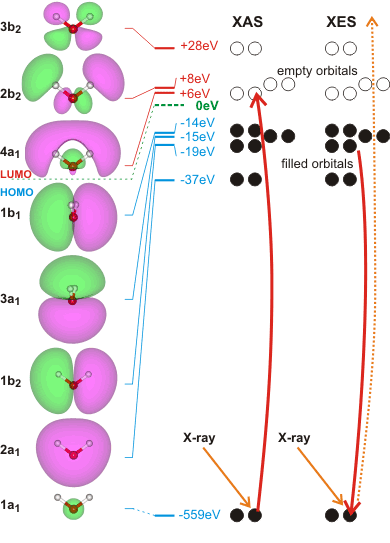
X-ray absorption spectroscopy (XAS) involves the absorption of high-energy photons to excite core (1s, 2s) electrons to unoccupied p-character valence levels. (see the molecular orbital energy levels left). The energies required are sensitive to the local environment mostly providing information concerning the hydrogen bond donating orbitals of the absorbing molecule at very short timescales (≈ 10−18s) [373, 690a, 1757]. The experimental XAS transition energies [3370] are
1a1 ![]() 4a1 534.0 ev
4a1 534.0 ev
1a1 ![]() 2b2 535.9 ev
2b2 535.9 ev
The energies given left are those calculated for isolated molecules using the Restricted Hartree-Fock wave function (RHF) using the 6-31G** basis set. Some electron movements are forbidden, such as 2a1 to half-empty1a1 hydrogen-bonding affects the energy levels.
XAS has been used to investigate the hydration of concentrated salt solutions [2170]. At high photon energy, expelled electrons have sufficient energy to escape from their atom (to the continuum), and at higher energies, these escaped electrons may produce signals due to backscattering. Care must be taken to avoid artifacts at the water-air surface due to desorption [1440]. Soft X‑ray (between 100 eV and 1 keV) absorption spectroscopy has been used on liquid microjets and flow-cells. This has enabled the general study of liquids and solutions [3306].
X-ray Raman scattering (XRS) gives similar results to XAS and involves the inelastic scattering of x-rays from the core electrons.
X-ray absorption spectrum of liquid water
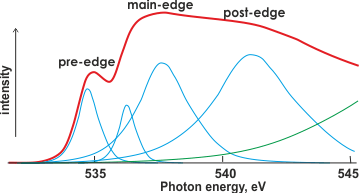
Shown right is the O K-edge (1s) XAS of liquid water (red) with possible underlying Gaussian (blue) and continuum (green) contributions.
The first peak in the X-Ray absorption spectrum (right) at about 535 eV (pre-edge) is due to excitation from the 1s orbital to the vacant O-H 4a1 antibonding orbital. It concerns water molecules with broken and weakened H-bonds. The post-edge bulge (~541 eV) is due to tetrahedral water molecules with intact hydrogen bonds. Assignment of these Gaussian peaks to electron transitions depends heavily on the underlying theory (for example, see the current dispute) as there is little structure in the experimental spectrum; this spectrum varies from run to run [690c], between methods and between different energies of the X-rays.
Thus, data fitting is error-prone. An interesting discussion of these differences has been published [834].
X-ray emission spectrum of water
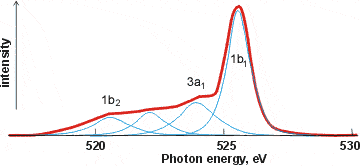
Related to XAS is the X-ray emission spectra (XES, shown right, [1757]) involving transitions from the three outermost occupied molecular orbitals 1b1, 3a1, and 1b2 to fill the vacancy (produced as above) in the 1a1 (1s) orbital [411]; peaks occurring in the 520-528 eV range and corresponding to instantaneous local structuring (≈ 3-4 ˣ 10−15 s). X-ray emission spectroscopy shows the presence within liquid water of two well-separated peaks (split from the lone-pair non-bonding 1b1 peak) that interconvert but do not broaden with changes in temperature [1639]. This strongly supports a two-state network model such as presented here, although it has been proposed that it may be alternatively due to ultrafast dynamics during the core-hole lifetime [2196]. Further work suggests that the splitting of the 1b1 peak possibly has more than two underlying hydrogen-bonding causes [4367].
X-ray spectroscopy has been combined with X-ray diffraction to opimize the structures [4475]. The information content in the X-ray spectroscopic data was found to be strongly complementary to that of X-ray diffraction, and dependent on specific structures that were consistent with the diffraction data.
Another improved X-ray technique is small-angle X-ray scattering (SAXS, [1757]) which is sensitive to density inhomogeneities in the nm range has confirmed the existence of two distinctly different hydrogen-bonded environments in liquid water [1757].
[Back to Top ![]() ]
]
a Consider, for example, the very different photographs obtained at night of cars on the road between the use of fast flash and a natural light long exposure. Short exposures show the cars but not the roads; long exposures show the roads but not the cars. An excellent illustration of the differences resulting in looking only at different aspects of a structure is given in [4202] with their depiction of the tale of “The Blind Men and the Elephant" by John Godfrey Saxe. [Back]
b There is evidence, however, that the spectra may be due to a continuous variation in the hydrogen bonding and not due to discrete but overlapping populations [875]. [Back]
Gaussian curve
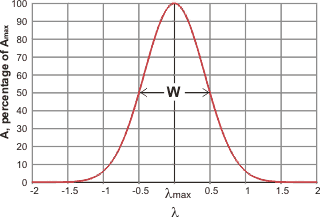
c Gaussian curve.There are two main ways of fitting vibrational spectra to underlying curves [4414],. A Gaussian curve (normal distribution curve) may be represented by the relationship:
![]()
where σ is the standard deviation and b is the offset.
therefore, for vibrational peaks,
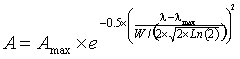
where A is the amplitude, Amax is the peak height, λ is the wavenumber, λmax is the wavenumber at the peak and W is the width of the peak at half-height, and the standard deviation (s) of the distribution s = W/(2 ˣ Ö(2 ˣ Ln (2)). Spectroscopic peaks can therefore be reduced to just three variable parameters, the position, the height, the width at half height.
The Gaussian curve assumes there are no outliers. It should be noted that although there is no theoretical reason why the actual sub-peaks should correspond precisely with Gaussian-shaped peaks, they generally fit well.
Lorentzian curve
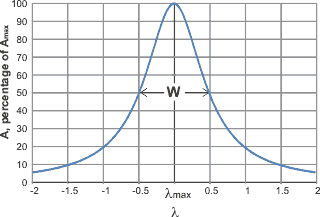
Lorentz distribution. (sometimes called the Cauchy distribution) The spectral distribution is sometimes better represented as a Lorentzian function
![]()
where Amax is the maximum peak height, λ is the wavenumber, λmax is the position of the maximum wavenumber, and ωL is the full width at half maximum height.
When the line widths are adjusted, Lorentz and Gaussian bands are essentially 'identical' for the upper 75% of the bands. Visual inspection cannot tell the difference. Neither are meant to represent large numbers of contributing peaks with different peak positions and widths. Gaussian curves are the best at representing this continuum of sub-peaks. As found, Lorentzian peaks can best represent peaks with extended bases but may give overall more significant residuals. A combination of the peaks in Voigt profiles does not improve the situation. It should be recognized that the best mathematical (least squares) fit might not be the best fit for the underlying structures. Also, there will probably be several fits that ly close to the best fit, where the natural noise in the data allows for no clear-cut favorite. Any good fit has small residuals, but even then, different fits may have acceptably small residuals, with the operator's choice between them being down to their personal choice. [Back, 2]
d 16O and 18O have zero nuclear spins. [Back]
e As an example of this, consider the 'average' structure of a person; nothing like a man or a woman, but somewhere in between. [Back]
f The rotational correlation time is the time it takes the average molecule to rotate one radian. It may be determined by dielectric spectroscopy. [Back]
g V. F. Sears, Neutron scattering lengths and cross-sections, Neutron News, 3 (1992.) 26-37. [Back]
h Raman versus infrared spectroscopy
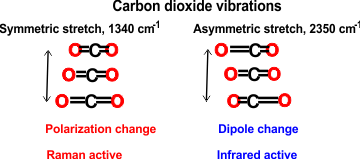 Infrared spectroscopy requires that the molecular dipole moment is affected by the vibration. In Infrared (IR) spectroscopy the electric vector of the rediation field oscillates with the same frequency as does the molecular dipole moment.
Infrared spectroscopy requires that the molecular dipole moment is affected by the vibration. In Infrared (IR) spectroscopy the electric vector of the rediation field oscillates with the same frequency as does the molecular dipole moment.
Raman spectroscopy requires that the molecular polarizability is affected by the vibration. In Raman spectroscopy, the molecule is exposed to an electric field so forcing the electrons and nuclei to move in opposite directions. and inducing a dipole moment. This dipole moment is proportional to the electric field strength and to the molecular polarizability. [Back]
Home | Site Index | Hydrogen bond | Water structuring | LSBU | Top
This page was established in 2005 and last updated by Martin Chaplin on 27 August, 2022