
Cluster equilibrium
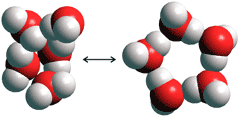
At ambient temperatures,
the icosahedral cluster equilibrium in water is shown rather idealistically
in the equation (ES![]() CS).
Complete clusters, without any pendant hydrogen bonding,
are likely to be rarely if ever found. It should be noted that
such a five or six (complete) shell cluster has 86% or 89% hydrogen-bonding (respectively), approximately
in line with that estimated by some in water [465a].
A dynamic range of partial structures (reducing the % hydrogen-bonding)
is expected together with extensive links to pendant molecules and
other clusters (increasing the hydrogen-bonding). A model, using
the significant liquid structure theory, estimates an average of
20 water molecules per flickering cluster gives the best fit over
a range of temperatures (0-100 °C) [600].
As the hydrogen bonding flickers between arrangements, the stability
of the expanded water dodecahedra (see below)
will vary [435].
CS).
Complete clusters, without any pendant hydrogen bonding,
are likely to be rarely if ever found. It should be noted that
such a five or six (complete) shell cluster has 86% or 89% hydrogen-bonding (respectively), approximately
in line with that estimated by some in water [465a].
A dynamic range of partial structures (reducing the % hydrogen-bonding)
is expected together with extensive links to pendant molecules and
other clusters (increasing the hydrogen-bonding). A model, using
the significant liquid structure theory, estimates an average of
20 water molecules per flickering cluster gives the best fit over
a range of temperatures (0-100 °C) [600].
As the hydrogen bonding flickers between arrangements, the stability
of the expanded water dodecahedra (see below)
will vary [435].
An effectively-infinite number of arrangements are possible, with even a dodecahedral (H2O)20 cluster having 30,026 symmetry-distinct hydrogen bond arrangements differing in energy by up to the equivalent of 40% of the hydrogen bond energies [464]). An extraordinarily complex potential energy surface is found, with lower energy arrangements tending to expand, whereas higher energy forms tending to pucker. The lower energy forms are more symmetrically arranged with the smallest net overall dipole and their partial-cluster dipoles being more stable [464]. c The higher energy forms are more asymmetric, with those with the largest net dipoles being the least stable. Fluctuations between these clusters lead to the flickering cluster phenomena. If the range of energies for the dodecahedral (H2O)20 cluster [464] is used for calculating the range of energies for the icosahedral (H2O)280 cluster, it is expected that differences in energy by up to the equivalent of 8% (40% ˣ 60/20 ˣ 20/280) of the hydrogen bond energies will be possible for differing hydrogen bond arrangements. As the temperature is lowered towards 0 °C and below, it is expected that a greater degree of cluster completion is to be found, flickering between structural forms (see animated gifs). There is likely to be a continuum of structures present. It is also possible that clusters can fuse together to form cylindrical clusters and to cover surfaces.
The agreement of the CS structure with the radial distribution
function indicates that it is by far the major contributor at
4 °C. Under pressure, the collapsed structure (CS)
may collapse further because only the one dodecahedron at the center
has collapsed in the cluster model (CS),
leaving three (12 quarters, icosahedrally arranged) mostly uncollapsed
on the periphery. As the density of ES is 0.94 g cm−3 and that of CS (with a quarter of the dodecahedral voids collapsed) is 1.00 g cm−3, then the collapse of these other three (equivalent) dodecahedral
voids (under pressure) will give a density of about 1.18 g cm−3;
similar to that of high-density amorphous ice when returned to ambient
pressure; so explaining the continuous nature of the
LDA![]() HDA process that occurs without breaking
the hydrogen bonds [394].
HDA process that occurs without breaking
the hydrogen bonds [394].
There are many changes to the structure of water that occur with increasing temperature. The water molecules gain energy, which is used to bend and break the hydrogen bonds. Due to the multiple nature of the hydrogen bonding around water molecules, central molecules in clusters are likely to resume unchanged hydrogen bonding after such breakage. However, peripheral molecules will be preferentially lost to other clusters, less structured environments, and interstitial sites. On raising the temperature, the size of ordered clusters decreases, the number of smaller clusters increases, the number of hydrogen bonds decreases, and the average distance between the water molecules increases.
(H2O)m ![]() (H2O)n + (H2O)m-n
(H2O)n + (H2O)m-n
Hhowever, there is always considerable hydrogen bonding, and it is likely that almost all molecules will be linked to almost all others by at least one intact chain of hydrogen bonds. Some hydrogen bonding, of the order of 1-2 hydrogen bonds per molecule dependent on the density, is evident even in supercritical water (>374 °C) [208].
Interesting phenomena, in the (interfacial) vicinal water that occurs at solid surfaces, are the apparent transitions in physical properties at the 'Drost-Hansen' temperatures (≈ 15 °C, ≈ 30 °C, ≈ 45 °C, ≈ 60 °C, and ≈ 75 °C) ([205a] but see the rebuttal [205b]). It is possible that these transitions are caused by the breakage of hydrogen bonds due to the increasing difference between the potential of the ordered vicinal and disordered bulk phases. This would then cause an incremental loss of order and restructuring of the water clusters and explain the pronounced thermal hysteresis in the effects. Note that the properties of bulk water have similar turning points. As examples, complex permittivity analysis shows a discontinuity at about 30 °C [1045], specific heat has a minimum at about 36 °C, compressibility has a minimum at about 46.5 °C, and the speed of sound has a maximum at about 73 °C). Gaseous solutes can create other turning points (for example, the presence of equilibrated air creates a turning point at 44 °C for the proton spin-lattice relaxation time in water, T1 [294]). It is not unreasonable that the changes in the clustering of water create these transitions within the interfaces. An interesting alternative, but non-exclusive, explanation involves thermal quantum effects that depend on the effective size of the molecules and the free volume space [724]. This quantum mechanical behavior has been supported by the anomalous thermal behavior of the laminar flow of water in a capillary with a colloidal silica sample [3268]. Other transitions occur in many ionic solutions on increasing their concentration to about molal concentrations [518] when the preferred (low concentration) water clustering starts to overlap at higher concentrations and indicating that at least 20 water molecules are associated with each ion's cluster.
Dodecahedral (H2O)20 clusters are at the center of the icosahedral water clusters. These are expanded when the hydrogen bonding is dominant and collapsed when the van der Waals dispersion interactions dominate. Under normal conditions, there will be an equilibrium between these forms.
Dodecahedral puckering
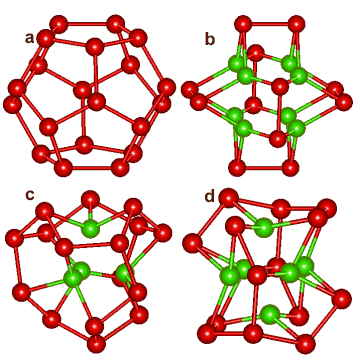
The central (H2O)20 dodecahedron of water molecules (a) in a water cluster can collapse in different ways.a Their oxygen atoms are depicted right, showing a collapse with 8 (b), 4 (c),or 6 (d) inner molecules (shown as green) producing cubic, tetrahedral or octahedral cavities, respectively.
Other collapsed structures are also possible (for example, with two inner molecules similar to the oxygen atoms in CO2 clusters).
Connectivity maps for the most (left, a) and
least (right, b) stable dodecahedral clusters
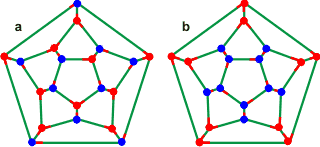
The connectivity map (Schlegel diagram) of the convex dodecahedron (a above) is shown left with red indicating oxygen atoms with both donor hydrogen bonds within the dodecahedral structure and blue indicating oxygen atoms with one donor hydrogen bonds pointing away from the structure. The most (a) and least (b) favored structures are shown [2111]. The most-stable positioning of the outward-oriented donor hydrogen atoms (blue) in an isolated cluster b, has three nearest neighbor double-donor and double-acceptor pairs [186]. The favored directions of (one set of) the hydrogen-bonded hydrogen atoms are also shown as short red lines [1441]. Also shown below are the connectivity maps of the dodecahedra showing the collapsed positions (pink circles with yellow circles giving an alternative) for 2 (f), 4 (d), 6 (e), and 8 (c) molecules. Alternative structures may be formed from all of these connectivity maps by rotation and reflection.
Connectivity maps for differently puckered dodecahedral clusters
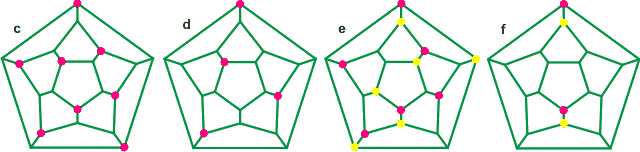
In water, it is expected that the more-central water molecules will be continually changing. There will be a range of collapsed structures, although some may be more stable than others; structure (b) was favored by molecular modeling. The figures (above) show the maximum amount of puckering when the non-bonded distance between the inner molecules (the edges of the holes) is the same as the bonded distance between two neighbors. In practice, a lesser degree of puckering is expected. With this maximal puckering, the central cavities have radii 1.71 Å, 2.01 Å, and 2.42 Å for tetrahedral, octahedral, and cubic cavities, respectively. Interactive structures are available using Jmol. The cavities may be occupied by ions, which interact with the puckered water molecules, in some cases forming magic number cluster ions.
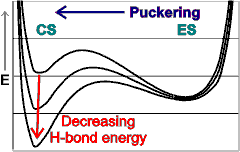
ES - CS puckering
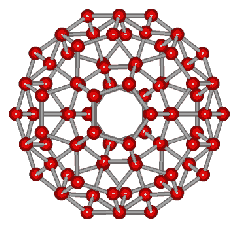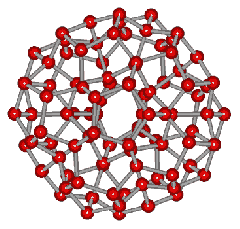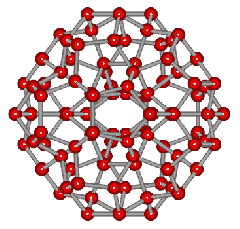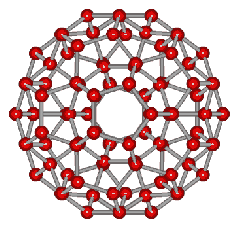
An icosahedral water cluster consisting of 280 water molecules has a central puckering dodecahedron. Only the oxygen atoms are shown. A full cluster also has 12 potential 100-water-molecule clusters surrounding the central 100 water molecule core. The puckering occurs with drops in the hydrogen bond energy (below left). Puckering not only changes the central dodecahedron but will flicker between new (surrounding) and old centers with the clusters disassembling and reforming as required, and as indicated in the animated figure below right. Thus, the cluster is self-replicating as any one cluster also contains the seeds for the forming up to 12 further clusters.
Potential energy diagram showing the minima due to the relative attraction of van der Waals forces and hydrogen bonding
Animated flickering cluster
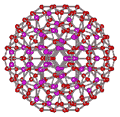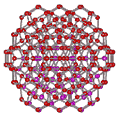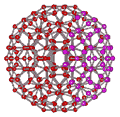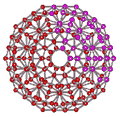
Radial positions of water molecules during puckering
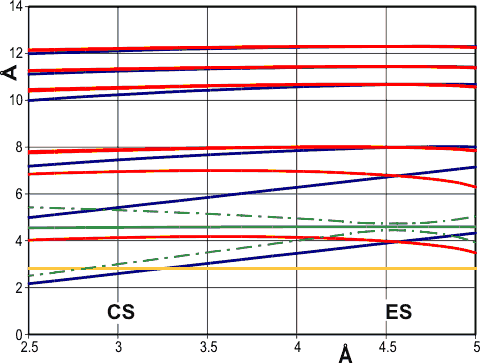
Puckering can occur with relatively small consequential distortion to the cluster as a whole. On the right is a graph showing the radial positions (vertical axis, — eight cubically arranged 14-molecule tetrahedra; — remaining twelve 14-molecule tetrahedra) in the six radial positions from the center (containing 1, 1, 3, 3, 3, 3 molecules respectively) with the non-bonded cubic box length of the puckered water (horizontal axis). To generate this graph, all hydrogen-bonded distances were held at 2.8 Å (—); also shown are the mean 2nd neighbor distances (—) and their range (—-—).
As the eight cubically arranged 14-molecule tetrahedra pucker inward (blue lines, moving to the left), the remaining twelve 14-molecule tetrahedra (red lines) first expand slightly before being dragged in. The large movement in the inner two puckering water molecules (lowest two blue lines) is severely attenuated in the remaining molecules in the cluster. The spherical angle coordinates (θ, φ) of all the molecules also fluctuate little (S.D. 0≈ 3°, average 0.33°) during the puckering. The total volume (indicated by the surface positions given by the outer three blue and red lines) reduces throughout the puckering. The ES structure corresponds to about the 4.6 Å horizontal position when all 14-molecule tetrahedra are equivalent. The CS structure corresponds close to 3 Å where the inner cubically-arranged puckered water molecules are at their minimum permissible non-bonded distance apart.
a It is also possible that dodecahedra can fuse to form tubes and cover surfaces. [Back]
b Although the difference in stability between hydrogen-bonding arrangements of the water's central dodecahedron ((H2O)20) within an icosahedral structure ((H2O)280) will be much smaller than for the isolated water dodecahedron, modeling studies show that a similar order of relative stability against puckering remains. The least stable hydrogen bond arrangement in the central dodecahedron has the greatest symmetry and largest net dipole moment. [Back]
c This can also be visualized as the form with the least number possible of free (non-hydrogen-bonded) H atoms on adjacent (hydrogen-bonded) water molecules. Of the ten free H-atoms in the most stable dodecahedral water cluster, (H2O)20 isomer, four are isolated, and six are contained in three isolated pairs of adjacent (hydrogen-bonded) water molecules, as shown above (a). [Back]
Home | Site Index | Equilibria gifs (379 KB) | Clusters | Ions | Magic number cluster ions | LSBU | Top
This page was established in 2000 and last updated by Martin Chaplin on 31 October, 2021