Water Complex Dielectric and Polarization

Microwave introduction
The complex dielectric permittivity
Polarization
Relative permittivity (dielectric constant) and polarization
Dielectric spectroscopy

The complex dielectric permittivity

A bimodal relaxation time expression is the most appropriate description of the dielectric properties of water [135].^{b, c}

(1)

where ε_r* is the complex permittivity, ε_S is the relative permittivity at low frequencies (static region), ε₂ is the intermediate relative permittivity, ε_∞is the relative permittivity at high frequencies (optical permittivity), ω is the angular frequency in radians.second⁻¹, τ_D and τ₂ are relaxation times, and i = . τ_D is relatively long (18 ps at 0 °C [135]), due primarily to the rotational relaxation within a hydrogen-bonded cluster, but reduces considerably with temperature (8 ps at 25 °C [2503 ]) as hydrogen bonds are weakened and broken. τ₂is small (≈ 1.0 ps [135], [2503] or 0.2 ps [343])^a and less temperature-dependent being determined primarily by the translational vibrations (near 200 cm⁻¹) within the hydrogen-bonded cluster [240].

Variation of the dielectric parameters with temperature

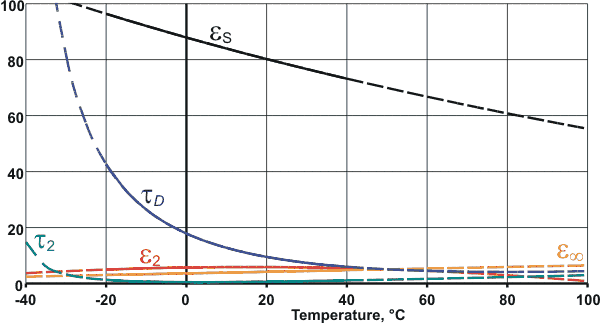
Plotted opposite are equations derived for pure water over the range for -20 °C ≈ +40 °C [683 ], extrapolated (dashed lines) to indicate trends; relaxation times are in ps. Further data has been published [1185 ].

Equation (1) may be simplified:

tan(delta) = loss factor/real permittivity — Tan(δ) = loss factor/real permittivity

and the complex permittivity rearranged to give the real permittivity and imaginary (the loss factor) parts:

The real part corresponds to the relative permittivity (dielectric constant):

and the imaginary part corresponds to the loss factor (Lf):

Loss factor = (static permittivity - intermediate permittivity) x angular frequency x first relaxation time /(1 + angular frequency squared x first relaxation time squared] +(intermediate permittivity - optical permittivity) x angular frequency x second relaxation time /(1 + angular frequency squared x second relaxation time squared

As (ε_S - ε₂) >> (ε_S - ε_∞) the permittivity may be approximated to within the accuracy of current instrumentation by:

(2)

As τ_D >> τ₂ and (ε_S - ε₂) >> (ε_S - ε_∞) the permittivity may be approximated by:

which shows minor deviations between about 100 - 1000 GHz that reduce with temperature increase. [Back to Top ]

Polarization

The polarization (P) of a substance is its electric dipole moment density (see also). It varies with the applied field (E = E_maxe⁻ⁱ^ωt) and the permittivity. The real part of the expression gives P,

P = E ε_r*ε₀

As E = E_max{cos(ωt) - i.sin(ωt)} and ε_r* = ε_r´ - i.Lf

P = E_max.ε₀(ε_r´ - i.Lf){cos(ωt) - i.sin(ω t)}

Therefore, taking only the real part:

P = E_max.ε₀{(ε_r´cos(ωt) - Lf sin(ωt)}

where ε_r´ varies with frequency as equation (2) above. This equation is equivalent to:

P = P_max.cos(ωt - δ)

where δ = atan(Lf/ε_r´) and P_max increases by a factor secant(δ). [Back to Top ]

Footnotes

^a The different values for τ₂ correspond to different frequency ranges, and the most appropriate relaxation time expression is trimodal [1247]. This analysis gives relaxation times τ_D, τ₂ and τ₃ at 25 °C of 8.26 ps, 1.05 ps and 0.135 ps respectively, and ε_S = 78.4, ε₂ = 5.85, ε₃ = 3.65, ε_∞ = 2.4. τ_D (19.3 GHz) corresponds to cooperative relaxation of long-range hydrogen-bond-mediated dipole-dipole interactions. τ₂ (150 GHz) is perhaps associated with dipole-dipole interactions due to the free rotation of water molecules having no more than one hydrogen bond. τ₃ (1.18 THz) is possibly associated with dipole-dipole interactions due to the free rotation of water molecules having no hydrogen bonds. These values may be compared with the bimodal relaxation times τ_D and τ₂ at 25 °C of 8.21 ps (19.3 GHz, corresponding to cooperative relaxation of long-range hydrogen-bond-mediated dipole-dipole interactions) and 0.392 ps (406 GHz, possibly associated with dipole-dipole interactions due to the free rotation of water molecules having broken hydrogen bonds), respectively, and ε_S = 78.4, ε₂ = 5.54, ε_∞ = 3.04 [1247]. A strong case has been proposed that the ionization of water can lead to the rearrangement of the water clusters and the values of both τ₁ and τ₂ [2423]. [Back]

Full dielectric spectrum, after ref. 1497 — Full dielectric spectrum (20 °C), from [1497], note the log-log scale.

mouse over for log-linear scale, from [4368]

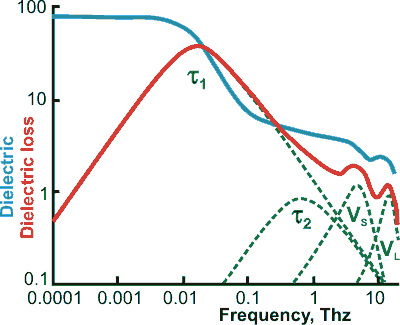
^b For use at higher frequencies up to 100 THz (that is, through the terahertz into the far infrared), two additional terms, representing the intermolecular stretch (V_S) and intermolecular librations (V_L), may be added [1497]. This spectrum has also been calculated [4415 ]. When the intermolecular stretching vibration is included, the following equation has been used [1563]

with the following values determined [1563]

	A_S, THz²	ω_S, THz	λ_S, THz	ε_∞
H₂O	1386	33.3	33.9	2.34
D₂O	1248	33.7	31.8	2.29
H₂¹⁸O	1184	31.1	26.7	2.28

The τ₁ and V_S peaks become lower and move to higher frequency at higher temperatures, whereas the V_S peak becomes higher and moves to lower frequency [3620].

[Back]

Bulk water aligns efficiently by an 11.7 THz laser field, using terahertz radiation. This giant THz Kerr effect, upon librational excitation (V_L), results in an efficient alignment of the bulk water molecules [3436].

Combined results from dielectric relaxation and neutron scattering measurements gave the 20-GHz peak (τ₁) as being due to molecular diffusion. In contrast, two high-frequency peaks at 0.15 (τ₂) and 2 THz originate from local motions of hydrogen and oxygen atoms, respectively [3321].

^c A 2015 model shows improved behavior in the supercooled region for use in atmospheric cloud measurements [2262]. [Back]