Effect of pH and ionic strength

Enzymes are amphoteric molecules containing a large number of acid and basic groups, mainly situated on their surface. The charges on these groups will vary, according to their acid dissociation constants, with the pH of their environment (Table 1.1). This will effect the total net charge of the enzymes and the distribution of charge on their exterior surfaces, in addition to the reactivity of the catalytically active groups. These effects are especially important in the neighbourhood of the active sites. Taken together, the changes in charges with pH affect the activity, structural stability and solubility of the enzyme.

Table 1.1. pK_as ^a and heats of ionisation ^b of the ionising groups commonly found in enzymes.

^a The pK_a (defined as -Log₁₀(K_a)) is the pH at which half the groups are ionised. Note the similarity between the K_a of an acid and the K_m of an enzyme, which is the substrate concentration at which half the enzyme molecules have bound substrate. (Back)

^b By convention, the heat (enthalpy) of ionisation is positive when heat is withdrawn from the surrounding solution (i.e., the reaction is endothermic) by the dissociation of the hydrogen ions. (Back)

There will be a pH, characteristic of each enzyme, at which the net charge on the molecule is zero. This is called the isoelectric point (pI), at which the enzyme generally has minimum solubility in aqueous solutions. In a similar manner to the effect on enzymes, the charge and charge distribution on the substrate(s), product(s) and coenzymes (where applicable) will also be affected by pH changes. Increasing hydrogen ion concentration will, additionally, increase the successful competition of hydrogen ions for any metal cationic binding sites on the enzyme, reducing the bound metal cation concentration. Decreasing hydrogen ion concentration, on the other hand, leads to increasing hydroxyl ion concentration which compete against the enzymes' ligands for divalent and trivalent cations causing their conversion to hydroxides and, at high hydroxyl concentrations, their complete removal from the enzyme. The temperature also has a marked effect on ionisations, the extent of which depends on the heats of ionisation of the particular groups concerned (Table 1.1). The relationship between the change in the pK_a and the change in temperature is given by a derivative of the Gibbs-Helmholtz equation:

          (1.12)

where T is the absolute temperature (K), R is the gas law constant (8.314 J M⁻¹ K⁻¹), DH is the heat of ionisation and the numeric constant (2.303) is the natural logarithm of 10, as pK_a's are based on logarithms with base 10. This variation is sufficient to shift the pI of enzymes by up to one unit towards lower pH on increasing the temperature by 50°C.

These charge variations, plus any consequent structural alterations, may be reflected in changes in the binding of the substrate, the catalytic efficiency and the amount of active enzyme. Both V_max and K_m will be affected due to the resultant modifications to the kinetic rate constants k₊₁, k_-1 and k_cat (k₊₂ in the Michaelis-Menten mechanism), and the variation in the concentration of active enzyme. The effect of pH on the V_max of an enzyme catalysed reaction may be explained using the, generally true, assumption that only one charged form of the enzyme is optimally catalytic and therefore the maximum concentration of the enzyme-substrate intermediate cannot be greater than the concentration of this species. In simple terms, assume EH⁻ is the only active form of the enzyme,

         [1.8]

The concentration of EH⁻ is determined by the two dissociations

          [1.9]

          [1.10]

with

          (1.13)

and

          (1.14)

However,

          (1.15)

therefore: 

          (1.16)

As the rate of reaction is given by k₊₂[EH⁻S] and this is maximal when [EH⁻S] is maximal (i.e., when [EH⁻S] = [EH⁻]₀):

          (1.17)

The V_max will be greatest when

          (1.18)

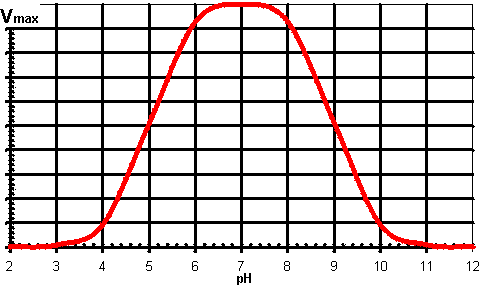
 therefore:

           (1.19) 

This derivation has involved a number of simplifications on the real situation; it ignores the effect of the ionisation of substrates, products and enzyme-substrate complexes and it assumes EH⁻ is a single ionised species when it may contain a mixture of differently ionised groups but with identical overall charge, although the process of binding substrate will tend to fix the required ionic species. It does, however, produce a variation of maximum rate with pH which gives the commonly encountered 'bell-shaped' curve (Figure 1.4). Where the actual reaction scheme is more complex, there may be a more complex relationship between V_max and pH. In particular, there may be a change in the rate determining step with pH. It should be recognised that K_m may change with pH in an independent manner to the V_max as it usually involves other, or additional, ionisable groups. It is clear that at lower non-saturating substrate concentrations the activity changes with pH may or may not reflect the changes in V_max. It should also be noted from the foregoing discussion that the variation of activity with pH depends on the reaction direction under consideration. The pH_optimum may well be different in the forward direction from that shown by the reverse reaction. This is particularly noticeable when reactions which liberate or utilise protons are considered (e.g., dehydrogenases) where there may well be greater than 2 pH units difference between the pH_optimum shown by the rates of forward and reverse reactions.

Figure 1.4. A generally applicable schematic diagram of the variation in the rate of an enzyme catalysed reaction (V_max) with the pH of the solution. The centre (optimum pH) and breadth of this 'bell-shaped' curve depend upon the acid dissociation constants of the relevant groups in the enzyme. It should be noted that some enzymes have pH-activity profiles that show little similarity to this diagram.

The variation of activity with pH, within a range of 2-3 units each side of the pI, is normally a reversible process. Extremes of pH will, however, cause a time- and temperature-dependent, essentially irreversible, denaturation. In alkaline solution (pH > 8), there may be partial destruction of cystine residues due to base catalysed b-elimination reactions whereas, in acid solutions (pH < 4), hydrolysis of the labile peptide bonds, sometimes found next to aspartic acid residues, may occur. The importance of the knowledge concerning the variation of activity with pH cannot be over-emphasised. However, a number of other factors may mean that the optimum pH in the V_max-pH diagram may not be the pH of choice in a technological process involving enzymes. These include the variation of solubility of substrate(s) and product(s), changes in the position of equilibrium for a reaction, suppression of the ionisation of a product to facilitate its partition and recovery into an organic solvent, and the reduction in susceptibility to oxidation or microbial contamination. The major such factor is the effect of pH on enzyme stability. This relationship is further complicated by the variation in the effect of the pH with both the duration of the process and the temperature or temperature-time profile. The important parameter derived from these influences is the productivity of the enzyme (i.e. how much substrate it is capable of converting to product). The variation of productivity with pH may be similar to that of the V_max-pH relationship but changes in the substrate stream composition and contact time may also make some contribution. Generally, the variation must be determined under the industrial process conditions. It is possible to alter the pH-activity profiles of enzymes. The ionisation of the carboxylic acids involves the separation of the released groups of opposite charge. This process is encouraged within solutions of higher polarity and reduced by less polar solutions. Thus, reducing the dielectric constant of an aqueous solution by the addition of a co-solvent of low polarity (e.g., dioxan, ethanol), or by immobilisation (see Chapter 3), increases the pK_a of carboxylic acid groups. This method is sometimes useful but not generally applicable to enzyme catalysed reactions as it may cause a drastic change on an enzyme's productivity due to denaturation (but see Chapter 7). The pK_a of basic groups are not similarly affected as there is no separation of charges when basic groups ionise. However, protonated basic groups which are stabilised by neighbouring negatively charged groups will be stabilised (i.e., have lowered pK_a) by solutions of lower polarity. Changes in the ionic strength (I) of the solution may also have some effect. The ionic strength is defined as half of the total sum of the concentration (c_i) of every ionic species (i) in the solution times the square of its charge (z_i);     i.e.        . I = 0.5S(c_iz_i²).
For example, the ionic strength of a 0.1 M solution of CaCl₂ is 0.5 x (0.1 x 2² + 0.2 x 1²) = 0.3 M. 
At higher solution ionic strength, charge separation is encouraged with a concomitant lowering of the carboxylic acid pK_as. These changes, extensive as they may be, have little effect on the overall charge on the enzyme molecule at neutral pH and are, therefore, only likely to exert a small influence on the enzyme's isoelectric point. Chemical derivatisation methods are available for converting surface charges from positive to negative and vice-versa. It is found that a single change in charge has little effect on the pH-activity profile, unless it is at the active site. However if all lysines are converted to carboxylates (e.g., by reaction with succinic anhydride) or if all the carboxylates are converted to amines (e.g., by coupling to ethylene diamine by means of a carbodiimide, see Chapter 3) the profile can be shifted about a pH unit towards higher or lower pH, respectively. The cause of these shifts is primarily the stabilisation or destabilisation of the charges at the active site during the reaction, and the effects are most noticeable at low ionic strength. Some, more powerful, methods for shifting the pH-activity profile are specific to immobilised enzymes and described in Chapter 3.

The ionic strength of the solution is an important parameter affecting enzyme activity. This is especially noticeable where catalysis depends on the movement of charged molecules relative to each other. Thus both the binding of charged substrates to enzymes and the movement of charged groups within the catalytic 'active' site will be influenced by the ionic composition of the medium. If the rate of the reaction depends upon the approach of charged moieties the following approximate relationship may hold,

          (1.20)

where k is the actual rate constant, k₀ is the rate constant at zero ionic strength, z_A and z_B are the electrostatic charges on the reacting species, and I is the ionic strength of the solution. If the charges are opposite then there is a decrease in the reaction rate with increasing ionic strength whereas if the charges are identical, an increase in the reaction rate will occur (e.g., the rate controlling step in the catalytic mechanism of chymotrypsin involves the approach of two positively charged groups, ⁵⁷histidine⁺ and ¹⁴⁵arginine⁺ causing a significant increase in k_cat on increasing the ionic strength of the solution). Even if a more complex relationship between the rate constants and the ionic strength holds, it is clearly important to control the ionic strength of solutions in parallel with the control of pH.